Механическая часть силового канала электропривода. Обобщенная графическая модель (совместная механичная характеристика электропривода)

Курс лекций по дисциплине

«Электрический привод»

МЕХАНИЧЕСКАЯ ЧАСТЬ СИЛОВОГО КАНАЛА ЭЛЕКТРОПРИВОДА. Математическое описание. Динамическое моделирование механической части силового канала электропривода

К основным составляющим элементам структурной схемы электропривода (ЭП) относятся:

1) силовой канал, по которому осуществляется транспорт потока энергии;

2) информационный канал, по которому реализуется управление отдельными элементами силового канала и передача информации об их состоянии.

В свою очередь силовой канал ЭП состоит из 2-х частей:

- механическая часть силового канала ЭП;

- электрическая часть силового канала ЭП.

Связывающим элементом, одновременно входящим в эти части, являетсяэлектромеханический преобразователь (ЭМП).

Механическая часть силового канала электропривода. Обобщенная графическая модель (совместная механичная характеристика электропривода)

Если в единой системе координат, в одном из квадрантов декартовой плоскости, построить механические характеристики электродвигателя (ЭД) и механизма (соответственно 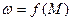и ), и 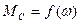для одних из тех же значений 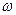определить арифметическую разность 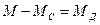, то мы получим динамический (избыточный) момент. Полученная зависимость: 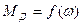- совместная механическая характеристика ЭП или обобщенная графическая модель электропривода.

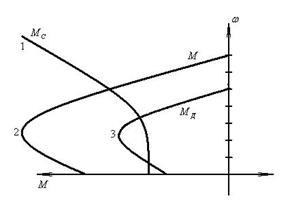
Рис.1 Совместная механическая характеристика электропривода

На рис.1:

1 - механическая характеристика механизма ;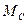

2 - механическая характеристика двигателя ;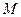

3 - совместная механическая характеристика .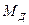

Каждая точка всех трех характеристик, взятых отдельно, описывает статические режимы.

С помощью совместной механической характеристики можно:

1) судить об устойчивости работы ЭП, с помощью коэффициента устойчивости :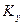

,

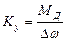где при 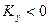- система устойчива, а при 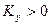- система неустойчива;

2) анализировать переходные процессы в ЭП. (строить характеристики ).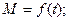

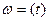Кроме того, при анализе механической части силового канала ЭП зачастую приходится учитывать упругость элементов механической части, наличие передаточных звеньев, результатом чего может являться неравенство скоростей вращения вала двигателя и вала механизма. Из-за этого, для последующего анализа механики ЭП, приходится использовать приведенные моменты сопротивления, моменты инерции, а также жесткости отдельных элементов.

Приведенный статический момент сопротивления :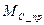

,

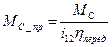где 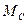- статический момент сопротивления;

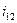- передаточное число,

;

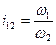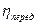- КПД передачи.

Приведенный момент инерции :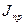

.

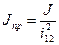Приведенная жесткость :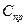

.

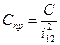Кроме того, для анализа механической части силового канала ЭП используются различные механические модели, которые, соответственно, имеют различное математическое описание. Наиболее общей и полной моделью механической части силового канала является двухмассовая механическая модель, на которой основные элементы представлены в виде 2-х вращающихся масс (двигатель и механизм).

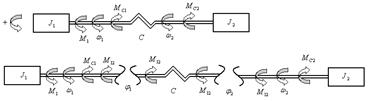
Рис.2 Схема двухмассовой механической модели

Составим систему уравнений, описывающих движение каждого их трех звеньев (1-я вращающаяся масса с моментом инерции 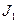, 2-я вращающаяся масса с моментом инерции 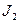, и звено связи). Используем метод, применяемый в механике, который состоит в том, что система расчленяется на отдельные звенья и, при этом, реальные звенья заменяются воздействием каждого звена друг на друга. В качестве меры этого воздействия используем момент упругости.

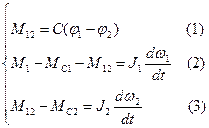
Таким образом, получили систему 3-х уравнений, которые представляют собой уравнения движения 2-х массовой модели.

Двухмассовая модель, как объект управления (аналоговый вариант)

В современной теории управления наиболее часто используется два вида переменных (две модели).

1. Переменные «входы-выходы». Суть этой модели заключается в том, что реальные физические величины, участвующие в системе, представляются в виде, так называемых, переменных «входы» и переменных «выходы», то есть, в измеряемых и нужных в данных системах физических величин. Этот вид модели хорош своей «физичностью», однако, в случаях сложных систем не всегда может быть использован.

2. Переменные «состояния». Система представляется в виде переменных, связанных с входами и выходами, и обеспечивает их совместимость, и, благодаря этому, удобное математическое описание весьма разнообразных величин.

Преимущество 2-го вида модели особенно ощутимо при работе со сложными системами с целью создания оптимальных алгоритмов управления.

1.2.1 Динамическая модель двухмассовой системы в переменных «входы-выходы». Структурная схема динамической модели

Для этого представим уравнения (1) - (3) в виде системы дифференциальных уравнений, где оператор 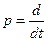обозначает 1-ую производную.

Кроме того, определим понятие «переменные», представляющие собой реальные воздействия, и, при этом, изменяющиеся в зависимости от поставленной перед собой задачи.

Выберем переменные, которые будем считать «входами» ( 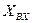), и переменные, которые будем считать «выходами» ( ).

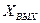В одной из очевидных постановок задачи входными переменными будут являться вращающий электромагнитный момент 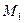, который формируется с помощью ЭД, а также моменты сопротивлени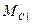й и 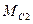, создаваемые, в основном, силами трения. Выходной переменной будет являться скорость второй массы .

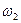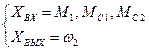
Продифференцируем уравнение (1):

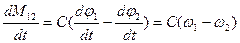
Тогда введя понятие «оператор», можно представить уравнения (1) - (3) в операторной форме:

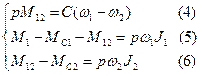
Решение задачи сводится к представлению графического образа системы, который состоит из совокупности графических образов отдельных звеньев и в них содержатся переменные ( 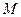, , 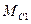, , 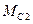, 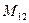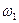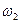), параметры ( 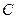, , 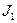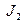) и оператор ( 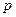). Условимся обозначать переменные стрелками; параметры и оператор, образующие алгебраические выражения заключать в прямоугольные рамки; а для алгебраического суммирования использовать окружности, иногда с секторами, при этом слагаемые обозначаются стрелками подходящими к не заштрихованным секторам окружности, вычитаемые - стрелками подходящими к заштрихованным секторам окружности, а сумму - стрелками отходящими от окружности.

Представим модель согласно уравнению (4).

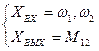
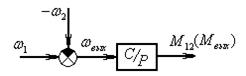
Рис.3а Динамическая модель ( )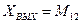

Модель, согласно уравнению (5):

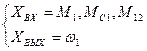
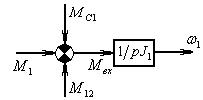
Рис.3б Динамическая модель ( )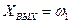

Модель, согласно уравнению (6):

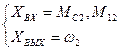
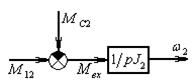
Рис.3в Динамическая модель ( )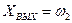

В графических образах все выражения, записанные в прямоугольных рамках, представляют собой выражения вида 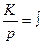(интегратор). Поэтому все три представленных звена можно отнести к звеньям интегрирующего типа. Для решения поставленный задачи объединим графические звенья в один графический образ - структурную схему системы. Для этого введем ещё одно обозначение - узел, который будем обозначать точкой, при этом, отходящие от одного узла стрелки соответствуют одной и той же переменной.

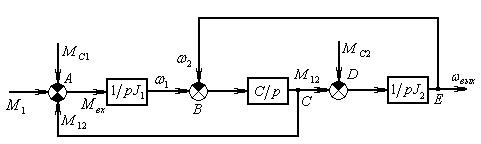
Рис.4 Структурная схема двухмассовой механическойсистемы в переменных «входы-выходы»

Выражение, заключённое в прямоугольные рамки, представляет собой отношение выходной величины к входной, и называется передаточной функцией звена.

Поставим перед собой задачу нахождения общей передаточной функции системы.

Для этого используют операцию агрегирования, т.е. свёртывания структурной схемы с целью представления её в виде одного звена.