Обобщенная электрическая машина. Координатные и фазные преобразования
Электромеханические преобразователи (ЭМП) являются основным звеном силового канала ЭП, которое непосредственно выполняет функцию преобразования электрической энергии в механическую, являясь, при этом, связующим звеном между электрической и механической частями силового канала.
В дальнейшем из всего многообразия ЭМП будем рассматривать Эл двигатели промышленного назначения.
В структуре электропривода ЭМП рассматривается в виде идеализированного ЭД, что означает:
1) ротор ЭД не обладает массой;
2) не имеет механических потерь;
3) жестко связан с реальным физическим ротором, относящимся к механической части ЭМП.
Такой идеализированный ЭД может быть представлен в виде электрического многополюсника, содержащим 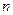 пар электрических выводов (
пар электрических выводов ( 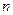 соответствует числу обмоток, фаз двигателя) и, кроме того, одну пару механических выводов. На механических выводах в результате электромеханического преобразования энергии при скорости вращения
соответствует числу обмоток, фаз двигателя) и, кроме того, одну пару механических выводов. На механических выводах в результате электромеханического преобразования энергии при скорости вращения 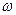 развивается электромагнитный момент
развивается электромагнитный момент 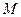 . Поэтому эти два вывода обозначаются
. Поэтому эти два вывода обозначаются 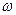 и
и 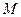 . Электромагнитный момент
. Электромагнитный момент 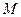 является выходным параметром ЭМП и, одновременно, выходным параметром для механической части силового канала. Угловая скорость
является выходным параметром ЭМП и, одновременно, выходным параметром для механической части силового канала. Угловая скорость 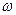 определяется условиями движения механической части, но для ЭМП обычно рассматривается как независимая переменная.
определяется условиями движения механической части, но для ЭМП обычно рассматривается как независимая переменная.
Механические переменные 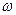 и
и 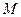 связывают ЭМП с механической частью в единую взаимосвязную систему. При этом все процессы в ЭД описываются системой уравнений электрического равновесия, число уравнений равно числу обмоток двигателя. Кроме того, в математическое описание ЭМП обязательно входит уравнение электромагнитного преобразования энергии и уравнение движения.
связывают ЭМП с механической частью в единую взаимосвязную систему. При этом все процессы в ЭД описываются системой уравнений электрического равновесия, число уравнений равно числу обмоток двигателя. Кроме того, в математическое описание ЭМП обязательно входит уравнение электромагнитного преобразования энергии и уравнение движения.
В современной теории ЭП в качестве обобщенной модели ЭМП обычно используют, так называемую, двухфазную модель; к ней можно привести абсолютно все виды и типы ЭМП. Такая модель – «Обобщенная электрическая машина» (рис.11).
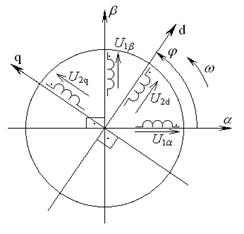
Рис.11 Обобщенная электрическая машина
На этой модели электрическая машина представлена в виде неподвижного статора с двумя обмотками, располагающимся вдоль неподвижных координат 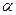 и
и 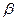 , а также вращающегося ротора с двумя обмотками, располагающимися вдоль вращающихся координат
, а также вращающегося ротора с двумя обмотками, располагающимися вдоль вращающихся координат 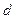 и
и 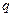 .
.
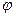 - угол поворота ротора;
- угол поворота ротора;
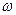 - скорость вращения ротора,
- скорость вращения ротора,
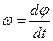 ;
;
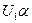 и
и 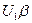 - напряжения на фазах обмотки статора;
- напряжения на фазах обмотки статора;
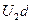 и
и 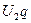 - напряжения на фазах обмотки ротора.
- напряжения на фазах обмотки ротора.
При этом уравнение электрического равновесия имеет вид:
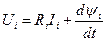 , (13)
, (13)
где 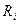 - активное сопротивление
- активное сопротивление 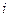 -ой обмотки;
-ой обмотки;
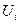 - напряжение на
- напряжение на 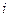 -ой обмотке
-ой обмотке
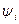 - потокосцепление
- потокосцепление 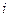 -ой обмотки
-ой обмотки
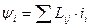 ;
;
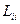 - собственные индуктивности,
- собственные индуктивности, 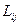 - взаимоиндуктивности.
- взаимоиндуктивности.
Необходимо отметить, что величина взаимоиндуктивностей зависит от угла поворота ротора 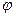 и, как следствие, от пространственного сдвига обмоток, т.е. является функцией скорости и времени. Это является физической причиной того, что ни у одной электрической машины значение
и, как следствие, от пространственного сдвига обмоток, т.е. является функцией скорости и времени. Это является физической причиной того, что ни у одной электрической машины значение 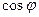 не может достигнуть 1.
не может достигнуть 1.
Для того чтобы ЭД любого вида и типа привести к представленной двухфазной модели этой машины производят координатные преобразования. Сущность этих преобразований сводится к тому, что для упрощения модели, функции статора, представленные в неподвижной системе координат 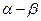 приводят к вращающейся системе координат
приводят к вращающейся системе координат 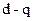 . А для того, чтобы вновь вернутся к реальному объекту систему
. А для того, чтобы вновь вернутся к реальному объекту систему 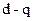 нужно привести к
нужно привести к 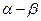 (
( 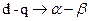 ).
).
Учитывая то, что большинство реальных ЭД включают в себя трехфазные статорные и роторные обмотки, для получения рассмотренной модели необходимо произвести прямые и обратные фазные преобразования, сущность которых сводится к следующему:
1) трехфазные в двухфазные 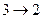 ,
, 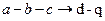 ;
;
2) двухфазные в трехфазные 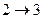 ,
, 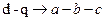 .
.
Дата добавления: 2015-05-08; просмотров: 1523;
