Одномассовая механическая модель силового канала электропривода

Если считать, что жесткость механической связи между 2-мя вращающимися массами бесконечно велика, то можно двухмассовую механическую модель представить в виде одномассовой.

Тогда:

,

,

,

.

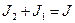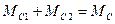Рис.9 Одномассовая механическая модель ЭП

Тогда система уравнений, описывающая двухмассовую механическую модель, сведётся к одному уравнению:

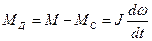(11)

В этом уравнении левая часть может быть графически представлена в виде 2-х функций и 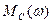, при этом, если строго следовать физическому смыслу этих функций, то - (статически-механическая характеристика ЭМП) будет располагаться в 1-м квадранте координатной плоскости, а функция 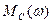, которая называется статическая механическая характеристика механизма, будет располагаться во 2-м квадранте.

В этом случае нахождение точки статического равновесия, а именно равенства , окажется невозможным. Поэтому обе характеристики для удобства анализа располагают в одном квадранте, чаще во 2-м (см. рис.1). Тогда уравнение (11) будет иметь вид арифметического уравнения.

При анализе механической части с помощью этого уравнения часто возникает проблема, связанная с недостатком каталожных данных о суммарном моменте инерции вращающихся частей, поэтому используют уравнение (11), записываемое в инженерных координатах.

В уравнении (11): 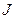- момент инерции равен произведению массы на квадрат приведенного радиуса инерции:

.

Тогда уравнение (11) примет вид:

Если представить: , где 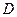- приведенный диаметр инерции, а массу представить через силу тяжести и ускорение свободного падения 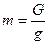, то уравнение примет вид:

(12)

Уравнения (11), (12) являются математическим описанием одномассовой механической модели, и называются, соответственно:

(11) - уравнение движения в классических координатах (классическое, основное);

(12) - уравнение движения в инженерных координатах.

В уравнении (12) выражение принято называть маховым моментом.

1.3.1 Одномассовая механическая модель как объект управления (аналоговый вариант). Динамическая модель одномассовой механической системы в переменных «входы-выходы»

Представим одномассовую модель механической системы в виде динамической модели в переменных «входы-выходы», имея в виду то, что система имеет следующее математические описание:

.

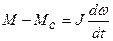Запишем уравнение в операторной форме:

.

Водные и выходные переменные:

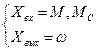
Рис.10 Структурная схема одномассовой механической модели

Передаточная функция звена:

.

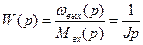ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ. Уравнения, описывающие электромеханические преобразователи. Механические характеристики электромеханических преобразователей в различных режимах их работы. Электромеханические преобразователи как объект управления. Энергетические соотношения в электромеханических преобразованиях

Под термином «электромеханический преобразователь» в дальнейшем будем подразумевать:

- ДПТ с НВ – двигатель постоянного тока с независимым возбуждением;

- АД – асинхронный двигатель;

- СД – синхронный двигатель;

- ДПТ ПВ - двигатель постоянного тока последовательного возбуждения.