Специальное представление линейных форм

Пусть V – унитарное пространство. Пусть "xÎV ® f(x)ÎC, такое что:

1) f(x₁ + x₂) = f(x₁) + f(x₂);

2) f(ax) = af(x).

Тогда говорят, что из V в C задан линейный функционал f или линейная форма f (fÎL(V, C)).

T°. Пусть fÎL(V, C), т. е. f – линейная форма, тогда существует единственный hÎV

такой, что f(x) = (x, h).

◀ Пусть {e_i} – ортонормированный базис V

"xÎV; ,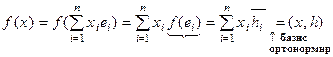

т.е. вектор h имеет координаты .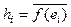

Единственность:Пусть f(x) = (x, h¹) = (x, h²) Þ (x, h¹ – h²) = 0; "xÎV.Возьмем x = h¹ – h² Þ (h¹ – h², h¹ – h²) = 0, т.е. h¹ = h² ▶

Примечание: в вещественном пространстве теорема и ее доказательство также справедливы, но в доказательстве не ставится знак комплексного сопряжения.

§2. Специальное представление полуторалинейных форм

Пусть "x, уÎV ® В(х, у)ÎС такое, что

;

.

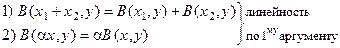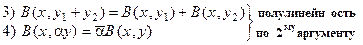Тогда говорят, что в унитарном пространстве задана полуторалинейная форма В(x, y).

(В евклидовом пространстве полуторалинейная форма становится билинейной).

Выберем в V базис {e_i}.

"уÎV .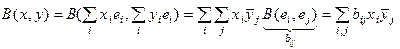

Действие формы В(x, y) однозначно определенно если известны элементы b_ij. Матрица В с элементами b_ij, называется матрицей полуторалинейной формы.

Тº. Пусть В – полуторалинейная форма в V. Тогда существует единственный

линейный оператор АÎL(V, V) такой, что В(x, y) = (x, Ay).

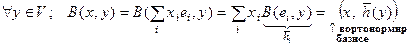◀ . Оказывается

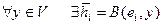, т.е. "yÎV ® hÎV. Таким образом, определен оператор h = Ay.

Линейность:

(x, A(a₁y₁ + a₂y₂)) = B(x, a₁y₁ + a₂y₂) = B(x, y₁) + B(x, y₂) = (x, Ay₁) + (x, Ay₂) =

= (x, a₁Ay₁) (x, a₂Ay₂) = (x, a₁Ay₁+ a₂Ay₂), т.е. А(a₁y₁ + a₂y₂) = a₁Ay₁+ a₂Ay₂.

Единственность:

Пусть B(x, y) = (x, A₁y) = (x, A₂y), тогда (x, A₁y – A₂y) = 0 Þ A₁y = A₂y "уÎV, т.е. A₁ = A₂ ▶

Тº. Пусть В – полуторалинейная форма в V. Тогда существует единственный

линейный оператор "АÎL(V, V)такой, что B(x, y) = (Ax, y).

◀ "хÎV 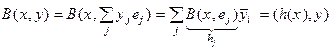или, что тоже определен оператор А такой, что h = Ax. При этом (A(a₁х₁ + a₂х₂), у) = В(a₁х₁ + a₂х₂, у) = a₁В(х₁, у) + + a₂В(х₂, у) = a₁(Ах₁, у) + a₂(Ах₂, у) = (a₁Aх₁ + a₂Aх₂, у) = A(a₁х₁ + a₂х₂) = a₁Aх₁ + a₂Aх₂ т.е. оператор А линейный.

Его единственность доказывается как в предыдущей теореме ▶

Примечание: в вещественном пространстве теорема и ее доказательство также справедливы, но в доказательстве не ставится знак комплексного сопряжения.

Тº. Если B(x, y) – полуторалинейная форма с матрицей В и А – линейный оператор

такой, что B(x, y) = (Аx, y), то в ортонормированном базисе матрица В^Т совпадает с

матрицей линейного оператора А.

◀ Пусть {e_i} ортонормированный базис V. Тогда

▶

Тº. Если B(x, y) – полуторалинейная форма с матрицей В и А – линейный оператор

такой, что B(x, y) = (x, Аy), то в ортонормированном базисе 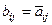. Доказать самостоятельно.

Примечание: Если А₁ – оператор из 1^й теоремы о спец. представлении и А₂ – из второй, то А₁ = .