Эрмитовы (самосопряженные) операторы

Def: Оператор "АÎL(V, V) действующий в унитарном пространстве называется эрмитовым (самосопряженным) оператором, если А^*=А.

Примечание: в евклидовом пространстве такой оператор называется самосопряженным.

Пусть А – произвольный линейный опреатор из L(V, V). Введем операторы А_R и А_I по правилу А_R = 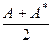; А_I = 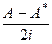, тогда А = А_R + iА_I и кроме того:

а) (А_Rx, y) = ( 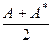x, y) = (x, ( 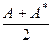)^*y) = (x, 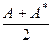y) = (x, A_Ry);

б) (А_Ix, y) = (( 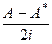)x, y) = (x, ( 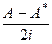)^*y) = (x, 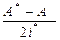y) = (x, A_Iy);

т.е . А_R и А_I эрмитовы.

Отсюда :

Т°. (о специальном представлении линейного оператора) "AÎL(V, V)

существуют эрмитовы операторы А_R и А_I такие, что А = А_R + iА_I (при

этом операторы А_R и А_I называются вещественной и мнимой частью

оператора А)

Def: Операторы A, BÎL(V, V) называются коммутирующими операторами если АВ = ВА.

Оператор 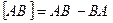называется коммутатором операторов А и В, и при этом 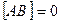– это необходимое и достаточное условие коммутируемости операторов А и В.

Т°. Произведение эрмитовых операторов А и В будет эрмитовым оператором тогда

и только тогда когда операторы А и В коммутируют (т. е. АВ = ВА).

◀ Так как операторы А и В эрмитовы, то:

(АВ)^* = В^*А^* = ВА (ф)

тогда:

а) Если АВ = ВА, то из (ф) (АВ)^*= АВ, т. е. оператор АВ – эрмитов.

б) Если АВ эрмитов, то (АВ)^*= АВ и из (ф) АВ = ВА т.е. операторы коммутируют ▶

Т°. Если А – эрмитов оператор, то "xÎV; (Ax, x)ÎR (здесь R - множество вещественных чисел).

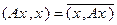◀ из свойств скалярного произведения (Ах, х) = (х, Ах) из эрмитовости оператора. Тогда 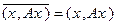, т.е. (Ax, x)ÎR ▶

Т°. Собственные числа эрмитового оператора вещественны.

◀ Пусть $xÎV, х ¹ 0 и $lÎС такие, что Ах = λх. Тогда:

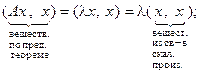(х, х) ³ 0, l – вещественно ▶

Т°. Собственные векторы эрмитового оператора, отвечающие различным

собственным значениям – ортогональны.

◀ Пусть Ах₁ = λ₁х₁, Ах₂ = λ₂х₂ и .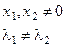

Тогда (Ах₁, х₂) = (λ₁х₁, х₂) = λ₁(х₁, х₂) равны как эрмитовы (х₁, Ах₂) = (х₁, λ₂х₂) = 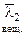(х₁, х₂) = = λ₂(х₁, х₂) и получено (λ₁ – λ₂)(х₁, х₂) = 0 Þ (х₁, х₂) = 0 ▶