Свойства сопряженных операторов.

1° Е^* = Е. ◀ (Ех, у) = (х, у) = (х, Еу) ▶

2° (А + В)^*=А^*+В^*.

◀ ((А + В)х, у) = (Ах + Вх, у) = (Ах, у) + (Вх, у) = (х, А^* у) + (х, В^* у) = (х, (А^* + В^*)у) ▶

3° (lА)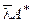^* = . ◀ (lАх, у) = l(Ах, у) = l(х, А^*у) = ▶

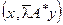4° (А^*)^*=А. ◀ (А^*х, у) = 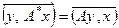= (х, Ау) ▶

5° (АВ)^*=В^*А^*. ◀ (АВх, у) = (А(Вх), у) = (Вх, А^*у) = (х, В^*(А^*)у) = (х, В^*А^*у) ▶

6° (А^–1)^*=(А^*)^–1.

Примечание: в евклидовом пространстве также справедливо все то, что сказано о сопряженном операторе, но свойство 3° имеет вид: (lА)^* = lА^*

Примечание: физики очень часто обозначают А^* как А⁺ (читается А – крест) и операцию называют эрмитовым сопряжением.