Матрица и оператор перехода

Пусть в линейном пространстве V задан базис {e₁, e₂, e₃, …, e_n} и другой базис {f₁, f₂, f₃, …, f_n}. Разложим векторы f_k по базису {e_i}: 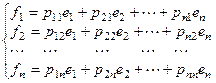, т.е. .

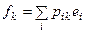Если координаты векторов нового базиса в старом записать в столбцы, получим матрицу линейного оператора Р который переводит векторы e_i в f_i (т.е. Рe_i = f_i). Этот оператор называется оператором переходаот базиса {e_i}к базису {f_i}, а его матрица называется матрицей соответствующего перехода.

Этот оператор невырожденный ибо {e_i}и {f_i}линейно независимы и, следовательно, имеет обратный оператор Р^–1, который является оператором перехода от базиса {f_i}к базису {e_i}. Таким образом, базисные векторы преобразуются с помощью оператора перехода Р_e→f:

Pe_i = f_i и Р^–1f_i = e_i.