Невырожденный линейный оператор
Линейный оператор А называется невырожденным если N(A) º {q} т.е. Ax = q Þ x = q. (в нейтральный переходит только нейтральный).
6°. Если оператор А невырожденный, то detA ¹ 0 для любого базиса.
◀ В самом деле, если aij – элементы матрицы оператора А в некотором базисе и Sj ее столбцы, то требование Ax = q Þ x = q можно записать в виде:
S1x1 + S2x2 + … + Snxn = 0 Þ x1 = x2 = … = xn = 0,
но это равносильно требованию линейной независимости столбцов матрицы оператора что (в свою очередь) равносильно требованию, что detA ¹ 0. ▶
7°. Если оператор А невырожденный, то существует и обратный ему линейный оператор А–1.
◀ Это следует из того что для невырожденной матрицы А существует обратная матрица и из взаимно однозначного соответствия между матрицами и линейными операторами. ▶
8°.Если к А существует обратный А–1, то detA ¹ 0.
◀ Ax = 0 (применим А–1), то:  Þ x = q. ▶
Þ x = q. ▶
Если dimV = n и А невырожденный оператор то rangA = n, дефект оператора А равен нулю.
¢ 8°.Невырожденный оператор осуществляет взаимно однозначные соответствие R на R.
◀ Ax = Ay Þ Ax – Ay = A(x – y) = q Þ x – y = q Þ x = y. ▶
9°.Если detA ¹ 0 то линейно независимые векторы переходят в линейно-независимые
векторы.
◀ Пусть e1, e2,…, en линейно независимые. Под действием А они переходят в Ae1, Ae2, …, Aen. Пусть a1Ae1 + a2Ae2 + … + anAen = q Þ A(a1e1 + a2e2 + … + anen) = q Þ
(a1e1 + a2e2 + … + anen) = q Þ a1 + a2 + … + an = 0. ▶
§7 инвариантные пространства
Подпространство V1 пространства V называется инвариантным относительно линейного оператора А если "xÎV1 Þ AxÎV1.
Примеры:
1) А – поворот вокруг оси Oz обычного трехмерного пространства: Инвариантные подпространства: плоскость xOy и ось Oz.
2) А – ортогональное проектирование того же трехмерного пространства на плоскость xOy. Инвариантные подпространства: плоскость xOy, все плоскости проходящие через ось Oz, сама ось Oz, все прямые в плоскости xOy и проходящее через начало координат.
3) В пространстве Pn многочленов степени не выше n, подпространства Pk "k, 0 £ k £ n инвариантны относительно оператора дифференцирования.
4) В любом пространстве V каждое подпространство инвариантно относительно тождественного и нулевого операторов.
5) В любом пространстве V само пространство V и подпространство, состоящее только из нулевого вектора {q} инвариантны относительно любого линейного оператора.
10°.Пересечение и сумма подпространств инвариантных относительно А также инвариантны относительно А.
◀ Пусть V1 и V2 – инвариантны относительно А.
Пусть xÎV1∩V2Þ xÎV1, xÎV2 Þ AxÎV1, AxÎV2 Þ AxÎV1∩V2.
Пусть xÎV1 + V2 Þ x = u + v, uÎV1, vÎV2 Þ Ax = Au  + Av
+ Av  Þ AxÎV1 + V2 . ▶
Þ AxÎV1 + V2 . ▶
11°.Если detA ¹ 0 и V1 инвариантно относительно оператора А, то V1 инвариантно и относительно оператора А–1.
◀ Пусть е1, е2,… еn – базис V1 Þ Aе1, Aе2,… Aеn – принадлежат V1 (из инвариантности), линейно независимы и, следовательно, образуют базис в V1 Þ "AxÎV1
х = a1Ae1 + a2Ae2 + … + arAer Þ А–1x = А–1(a1Ae1 + a2Ae2 + … + arAer) =
= a1e1 + a2e2 + … + arerÎV1. ▶
12°.Если V1 инвариантно относительно оператора А, то V1 инвариантно и относительно оператора  , где
, где  – произвольный полином.
– произвольный полином.
◀ Действительно, если  то из инвариантности V1 следует, что
то из инвариантности V1 следует, что  и, следовательно,
и, следовательно,  ▶
▶
Отметим, в частности, что подпространство инвариантное относительно оператора А, инвариантно и относительно оператора  при любом числе
при любом числе 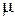 . Верно и обратное утверждение: если подпространство инвариантно относительно оператора
. Верно и обратное утверждение: если подпространство инвариантно относительно оператора  , то оно инвариантно и относительно А, ибо
, то оно инвариантно и относительно А, ибо  . Очевидно, что все пространство и пространство, состоящее из нейтрального элемента, суть инвариантные подпространства. Нетривиальными примерами инвариантных подпространств могут служить, например, подпространства, натянутые на один или несколько собственных векторов оператора А.
. Очевидно, что все пространство и пространство, состоящее из нейтрального элемента, суть инвариантные подпространства. Нетривиальными примерами инвариантных подпространств могут служить, например, подпространства, натянутые на один или несколько собственных векторов оператора А.
Действительно, пусть векторы 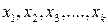 – собственные векторы оператора А и Р натянутое на них подпространство. Тогда любой вектор
– собственные векторы оператора А и Р натянутое на них подпространство. Тогда любой вектор  , может быть представлен в виде
, может быть представлен в виде  и потому:
и потому:
 .
.
Среди чисел 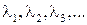 могут быть равные. В случае, если все собственные значения оператора различны, указанными подпространствами исчерпываются все инвариантные подпространства оператора.
могут быть равные. В случае, если все собственные значения оператора различны, указанными подпространствами исчерпываются все инвариантные подпространства оператора.
Другим важным типом инвариантных подпространств являются циклические подпространства. Для определения этого понятия рассмотрим следующую конструкцию. Пусть дан вектор  . Построим систему векторов:
. Построим систему векторов:  . Ясно, что в этой системе когда то в первый раз встретится вектор
. Ясно, что в этой системе когда то в первый раз встретится вектор  , являющийся линейной комбинацией предыдущих
, являющийся линейной комбинацией предыдущих 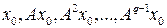 .
.
Циклическим подпространством Q, порожденным вектором  , называется подпространство, натянутое на векторы
, называется подпространство, натянутое на векторы 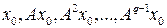 . Так как векторы
. Так как векторы 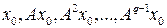 линейно независимы, то они образуют базис циклического подпространства Q и потому размерность Q равна показателю степени q.
линейно независимы, то они образуют базис циклического подпространства Q и потому размерность Q равна показателю степени q.
13˚. Циклическое подпространство, порожденное вектором  , есть наименьшее инвариантное подпространство, содержащее
, есть наименьшее инвариантное подпространство, содержащее  , т.е. оно само инвариантно и содержится во всяком инвариантном подпространстве, содержащем
, т.е. оно само инвариантно и содержится во всяком инвариантном подпространстве, содержащем  .
.
Действительно, пусть Aqx0 = γ0x0 + … + γ0Aq–1x0 и пусть уÎQ. Тогда
у = с0x0 + с1Аx0 + … + сq–2Aq–2x0 + сq–1Aq–1x0;
Ау = с0Аx0 + с1А2x0 + … + сq–2Aq–1x0 + сq–1Aqx0 = с0Аx0 + с1А2x0 + … + сq–2Aq–1x0 +
+ сq–1(γ0x0+γ1Аx0 + … + γq–1Aq–1x0) = 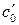 x0 +
x0 +  Аx0 + … +
Аx0 + … +  Aq–2x0ÎQ.
Aq–2x0ÎQ.
Тем самым инвариантность Q доказана.
Далее, пусть Q¢ какое-либо инвариантное подпространство, содержащие x0. Тогда x0ÎQ¢; Аx0ÎQ¢, …, Aq–1x0ÎQ¢ и, следовательно Q Ì Q¢, что доказывает минимальность Q среди инвариантных подпространств, содержащих x0.
Отметим для дальнейшего, что любое циклическое по отношению к оператору А подпространство, порожденное вектором x0, будет циклическим и по отношению к оператору А – mЕ при любом численном значении для m. Действительно, каждое инвариантное по отношению к А подпространство будет инвариантным и для А – mЕ и обратно, и, следовательно, минимальные инвариантные подпространства, содержащие x0, должны совпадать.
14°. Пусть А произвольный линейный оператор в V, (dimV = n) и пусть V = V1⊕ V2, где V1 и V2– инвариантные подпространства оператора А. Пусть е1, е2,…, еr – базис в V1, еr+1, еr+2, …, еn – базис в V2. Тогда в силу инвариантности V1 и V2 относительно А:
Aei = a1ie1 + a2ie2 + … + arier, i = 1, 2, …, r
Aei = ar+1, i er+1 + … + an i en, i = r + 1, r + 2, …, n.
И, следовательно, матрица линейного оператора Аимеет вид
 .
.
Говорят, что матрица А имеет блочную структуру (распадается на клетки):  .
.
Дата добавления: 2015-05-05; просмотров: 1637;
