Метод Квайна-Мак Класки
Это метод, ориентированный на числовое задание ФАЛ в виде кубического комплекса, состоящего из 0-кубов. Метод представляет собой формализованный на этапе нахождения простых импликант метод Квайна. Основной недостаток метода Квайна – необходимость выполнения полного сравнения (склеивания) всех первичных импликант. В случае большого их количества сложность этого сравнения существенно возрастает. В рассматриваемом методе все исходные n-кубы разбиваются на непересекающиеся подгруппы по количеству единиц в кубе. Пусть, например, задана функция:
f СДНФ(x1x2x3x4) = V (2, 3, 4, 6, 9, 10, 11, 12)
Сформируем кубический комплекс K, состоящий из 0-кубов.
K=(0010, 0011, 0100, 0110, 1001, 1010, 1011, 1100)
Выполнив разбиение комплекса K на группы, получим:
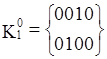
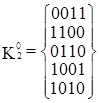
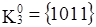
Попарное сравнение можно проводить только между соседними по номеру группами кубов, так как кубы, порождающие новые кубы, должны иметь кодовое расстояние, равное 1. В результате сравнения кубов получим:
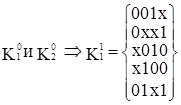
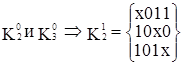
После выполнения первого шага алгоритма простых импликант не выявлено. Полученные 1-кубы разобьем на n групп кубов в зависимости от местоположения свободной координаты в кубе.
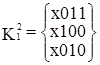
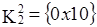
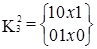
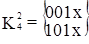
Далее выполняется сравнение кубов внутри каждой из групп. В результате чего могут быть получены 2-кубы, которые, в свою очередь, аналогично 1-кубам будут объединены в группы по совпадению свободных координат и вновь выполнено сравнение. На каждом шаге сравнения выявляются кубы, не участвовавшие в образовании новых кубов, и исключаются из дальнейшего упрощения. Для рассматриваемого примера сравнение в группах 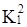 …
… 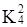 привело к образованию двух новых кубов х01х и х01х и кубов, не образовавших новых {х100, 0х10, 10х1, 01х0}.
привело к образованию двух новых кубов х01х и х01х и кубов, не образовавших новых {х100, 0х10, 10х1, 01х0}.
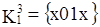
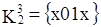
Дальнейшее сравнение не приводит к формированию новых кубов 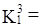
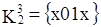 . Таким образом, получено множество простых импликант:
. Таким образом, получено множество простых импликант:
fсокр.ДНФ={х100, 0х10, 10х1, 01х0, х01х}
Далее аналогично методу Квайна строится импликантная таблица (табл.15). Формирование минимального покрытия сводится к выявлению обязательных простых импликант и на их основе построению тупиковых форм.
Таблица 15.
| Простые импликанты | Конститутиенты единицы | |||||||||
| х100 | * | * | ||||||||
| 0х10 | * | * | ||||||||
| 10х1 | * | * | ||||||||
| 01х0 | * | * | ||||||||
| х01х | * | * | * | * |
Из таблицы следует, что простые импликанты x100, 10x1, x01x являются обязательными. Оставшиеся две простые импликанты не являются обязательными и образуют следующие две тупиковые формы.
f МДНФ = {х100, 10х1, х01х, 0х10} – I тупиковая форма.
f МДНФ = {х100, 10х1, х01х, 01x0} – II тупиковая форма.
Алгоритм извлечения (Рота)
Метод Рота ориентируется на задание логической функции в форме произвольного кубического покрытия, что позволяет упростить процесс подготовки выражения для минимизации. Достоинство алгоритма Рота – полная формализация действий на всех этапах минимизации функции.
Дата добавления: 2015-05-05; просмотров: 1414;
