Минимизация не полностью определенных ФАЛ

Если при синтезе логической схемы, реализующей некоторую ФАЛ n переменных, окажется, что некоторые наборы из общего числа 2ⁿ никогда не смогут появиться на входах схемы, то данная логическая функция не определена на этих наборах. Тогда 2ⁿ наборов переменных можно подразделить на три группы: наборы, на которых функция принимает единичное значение L, нулевое значение D и группа наборов, на которых функция не определена N (неопределенные наборы). ФАЛ, содержащая неопределенные наборы, называется неполностью или частично определенной. Неопределенные наборы могут быть использованы для улучшения качества минимизации. При этом неопределенные наборы (при минимизации, например, картами Вейча, Карно) могут участвовать в образовании контуров как с единичными, так и с нулевыми наборами. Это приводит к формированию более простой минимизированной логической функции.

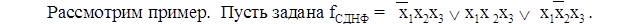
	x2
x1	1		1	*
	*		*
	x 3

Звездочками на карте (рис. 21) отмечены наборы на которых функция f не определена. Если не учитывать неопределенные наборы, то записать минимальная форма будет иметь вид: 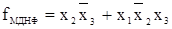. В случае если неопределенные наборы участвуют в образовании контуров, а следовательно, и f_МДНФ, то функция примет следующий вид: 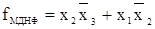. Таким образом, схемная реализация полученной f_МДНФ будет дешевле.

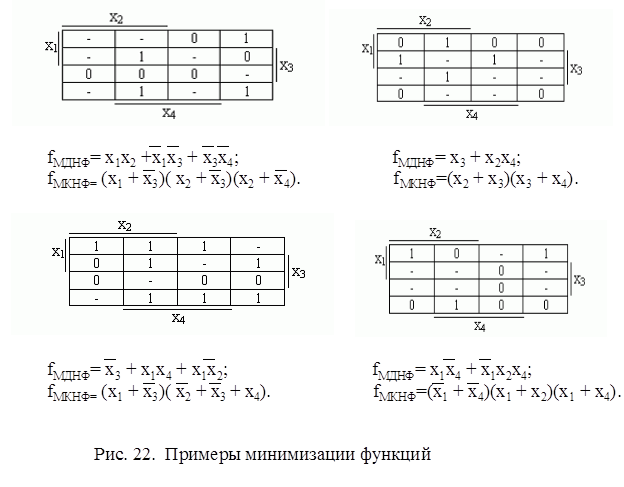
Приведем несколько примеров минимизации частичных булевых функций: