Кубическое задание функций алгебры логики.
Как следует из рассмотренного выше, функция алгебры логики (булева функция) может быть задана:
§ аналитически (системой булевых функций);
§ словесным описанием;
§ таблицей истинности;
§ картами (диаграммами) Венна, Вейча, Карно;
§ логической схемой;
Более компактной формой записи функций алгебры логики является форма, когда вместо полного перечисления всех конъюнкций (дизъюнкций) используют номера наборов, на которых функция принимает единичное значение. Так, например, форма записи f(x1x2x3)=V F(0,2,3) означает, что функция от трех переменных принимает единичное значение на 0, 2 и 3 наборах из таблицы истинности. Такая форма записи называется числовой.
Некоторые методы минимизации ориентируются на задание булевой функции в виде кубического покрытия. При этом логическая функция удобно интерпретируется с использованием ее геометрического представления. Так, функцию двух переменных можно интерпретировать как плоскость, заданную в системе координат х1х2. Получится квадрат, вершины которого соответствуют комбинациям переменных. Для геометрической интерпретации функции трех переменных используется куб, заданный в системе координат х1х2х3 .
Новое представление булевой функции получается путем отображения булевой функции n переменных на n-мерный куб (n-куб).
Для отображения булевой функции n переменных на n – кубе устанавливается соответствие между членами СДНФ и вершинами n - куба. На n- кубе определим координатную систему с координатами (e1,......,en), ei=0,1. Установим соответствие между членом СДНФ x1e1 x2e2... xnen и некоторой вершиной e1 ,e2 , ...., en куба. При этом xiei = xi если ei=1, и xiei = xi если ei=0.


Рис.23. Геометрическое представление функции двух и трех переменных
 Для отображения булевой функции n переменных на n – кубе устанавливается соответствие между членами СДНФ и вершинами n - куба. На n- кубе определим координатную систему с координатами (e1,......,en), ei=0,1. Установим соответствие между членом СДНФ x1 x2 ... xn и некоторой вершиной e1 ,e2 , ...., en куба.
Для отображения булевой функции n переменных на n – кубе устанавливается соответствие между членами СДНФ и вершинами n - куба. На n- кубе определим координатную систему с координатами (e1,......,en), ei=0,1. Установим соответствие между членом СДНФ x1 x2 ... xn и некоторой вершиной e1 ,e2 , ...., en куба.
Каждый набор при кубическом задании ФАЛ называется кубом.
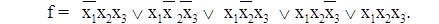
| Таблица 14. | ||||
| х1 | х2 | х3 | f | |
| - | ||||
Как следует из таблицы истинности, функция f образована на трех группах наборов переменных: L={3,4,5,6,7}, D={0,2} и N={1}.
Конъюнкции максимального ранга (конститутиенты единицы) принято называть 0-кубами. Множество 0- кубов образуют кубический комплекс

 011
011
К0 = 101
Над 0-кубами, кодовое расстояние которых равно 1, выполняется операция склеивания, в результате которой образуются новые кубы, содержащие свободные координаты. Свободная (независимая) координата может принимать как нулевое, так и единичное значение, остальные компоненты называются связанными.. Куб, содержащий свободные координаты, покрывает кубы, на которых он образован. Куб с одной независимой координатой х называется кубом первой размерности и в геометрическом представлении это ребро, покрывающее обе вершины. Кубы, образующиеся в результате последовательного выполнения операции склеивания, назовем r-кубами, где r – размерность полученного куба.
|
Геометрическая интерпретация сказанного показана на рис. 24. В результате склеивания кубов 101 и 111 (0-кубы, вершины) образован 1-куб 1x1 (ребро), а 1-кубов 00x и 10х - 2-куб х0х (грань).
Рис. 24. Образование новых кубов.
Кубическое представление ФАЛ позволяет обойтись тремя переменными 0,1,х вместо х1, х2,...,хn .
Количество свободных координат в кубе определяет его размерность r, чем больше r тем больше свободных координат и тем меньше входов будет иметь схема.
Цена схемы оценивается количеством входов: 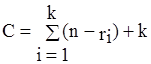 ,
,
где k-количество полученных кубов, n-ri - количество единичных и нулевых значений i-го куба.
Два r-куба могут образовать r+1-куб, если в этих r-кубах все координаты, в том числе и свободные, совпадают, за исключением лишь какой-либо одной, которая в этих кубах имеет противоположное значение.
Ниже приведено изображение куба, соответствующего булевой функции от четырёх переменных (гиперкуб).
Как следует из рисунка, геометрическое представление 4-куба уже довольно сложное. Поэтому для функций, зависящих более чем от четырёх переменных, предпочтительным является аналитическое представление булевых функций.
 |
Рис. 25. Геометрическое представление функции четырех переменных
Дата добавления: 2015-05-05; просмотров: 1526;

