Специальные логические операции алгоритма извлечения: *,∩ ,#.
Реализация алгоритма извлечения осуществляется на основе специальных логических операций, которые позволяют полностью формализовать процесс получения минимальной формы.
Операция умножения кубов (*).
Операцияпроизведения кубов а=а1а2...аn и b=b1b2...bn обозначается как с=а*b и служит для образования r-куба, противоположные (r-1) – грани которого содержатся в кубах а и b. Предварительные координаты куба c определяются в соответствии с таблицей.
 * *
| х | ||||
| y | |||||
| у | ||||
| x | х |
î ______________Ú_________________þ
bi
Окончательно координаты куба формируются:
 m(a1*b1)m(a2*b2) ... m(an*bn,) если ai*bi=y только для одного i
m(a1*b1)m(a2*b2) ... m(an*bn,) если ai*bi=y только для одного i
a*b=
Æ, если ai*bi=y, для i ³ 2
где m(ai*bi) – окончательная i-я координата куба с, m(0)=0, m(1)=1, m(x)=x.
 Эта операция соответствует операции склеивания: образуется новый r-куб, если кодовое расстояние двух исходных кубов равно 1. Рассмотрим некоторые примеры.
Эта операция соответствует операции склеивания: образуется новый r-куб, если кодовое расстояние двух исходных кубов равно 1. Рассмотрим некоторые примеры.
1) 011 2) 11х
*001*01х
0y1 Þ 0x1– ребро покрывает две вершины у1х Þ х1х – грань
3) 0х1 4) х1х
*1х0 *011
уху Þ Æ – две координаты имеют значение у. 011
Операция пересечения кубов (∩).
Операция пересечения кубов а=а1а2...аn и b=b1b2...bn обозначается как с=а∩b и служит для выделения куба с=с1с2...сn , являющегося общей частью кубов а и b. Координаты с1с2...сn определяются согласно таблице:
∩ 
| x | ||||
| Æ | |||||
| Æ | ||||
| x | x |
î______________Ú_________________þ
bi
 m(a1∩b1)m(a2∩b2) ... m(an∩bn,)
m(a1∩b1)m(a2∩b2) ... m(an∩bn,)
a∩b=
Æ, если существует такое i, для которого ai ∩ bi =Æ
где m(ai*bi) – окончательная i-я координата куба с, m(0)=0, m(1)=1, m(x)=x.
Рассмотрим примеры.
1) Ç100 2) Ç1х0
00110х
10Æ Þ Æ общей части у 100 Þ 100 общая часть
кубов нет; (вершина) кубов (рёбер);
3) Çх1х 4) Ç0хх
0хх 0х0
01х Þ 01х общая часть – ребро; 0х0 ( совпадает с
операцией *).
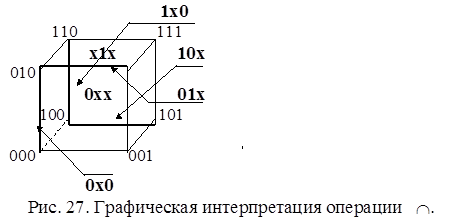
Операция вычитания кубов (#).
Операция вычитания из куба а=а1а2...аn куба b=b1b2...bn обозначается как с=а#b и служит для удаления из куба а общей части кубов а и b.
Координаты куба с формируются согласно таблице:
# 
| x | ||||
| z | y | z | |||
| y | z | z | ||
| x | z |
î ______________Ú_________________þ
bi
 Æ, если " i, аi#bi=z; z-означает, что координаты совпадают;
Æ, если " i, аi#bi=z; z-означает, что координаты совпадают;
c=а#b= a, если $ i, аi#bi=y, у-означает, что координаты противоположны;
U а1а2...аi-1 ai аi+1 ... аn, если ai равно 0 или 1 для одного или
i=1 нескольких i.
По этим ai-координатам производится объединение (U) кубов, получаемых в результате замены в кубе а символа х на соответствующее значение (0,1) координаты ai. Рассмотрим примеры выполнения операции #.
1) #х1х 2) #х1x
x11110
 zz0 Þ x10 0z1 Þ 01x
zz0 Þ x10 0z1 Þ 01x
3) #хx1 4) #х11 x11
x10 xx1
 z0y Þ xx1 zzz Þ Æ
z0y Þ xx1 zzz Þ Æ

5) # 0ххx
хх01
 zz10 Þ 0x1x
zz10 Þ 0x1x
0xx0
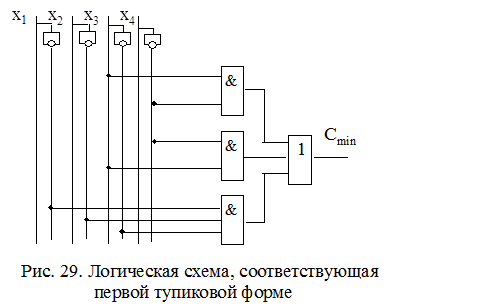
Далее рассмотрим алгоритм извлечения (Рота) на примере минимизации булевой функции, заданной покрытием С0.
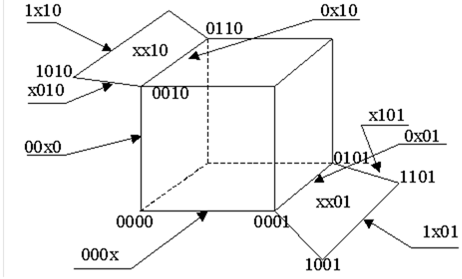
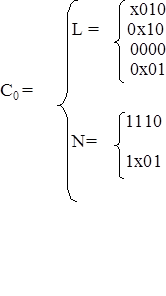
Рис. 29. Геометрическое задание исходного покрытия.
Исходное покрытие С0 задано объединением множеств кубов L и N. Кубы комплекса N- это наборы на которых функция не определена и включаются в покрытие ради возможного дополнительного упрощения комплекса L в процессе минимизации. Минимальное покрытие комплексов L и N, С min – называется К- покрытием L.
Общий алгоритм построения минимального К-покрытия называется алгоритмом извлечения и состоит в следующем:
▪ нахождении множества Z простых импликант комплекса К;
▪ выделении L-экстремалей на множестве Z;
▪ применении алгоритма ветвления при отсутствии L-экстремалей;
▪ нахождении абсолютно минимального покрытия из некоторого множества избыточных покрытий.
1. Нахождение множества простых импликант.
Преобразование исходного покрытия С0 комплекса К в множество простых импликант Z осуществляется с помощью операции умножения кубов.В результате первого шага (С0*С0) предусматривается выявление как новых кубов Сy (первой и более высокой размерности), так и кубов, которые не образуют новых кубов (включаются в множество Z0). Из полученных новых кубов образуется множество А1. В1=С0-Z0. Для следующего шага формирования множества Z формируется множество С1=А1U В1. Для уменьшения мощности множества кубов С1 выполним операцию поглощения (удаления) кубов образующих множество С1 кубами из множества А1 (А1ÍС1). Для рассматриваемого примера получим:
Таблица 16.
| С0*С0 | х010 | 0х10 | 0х01 | 1x10 | |||
| х010 | - | ||||||
| 0х10 | - | ||||||
| 00у0 | 00у0 | - | |||||
| 0х01 | ø | ø | 000у | - | |||
| 1у10 | у110 | ø | ø | - | |||
| 1х01 | ø | ø | ø | ух01 | ø | - | |
| А1 | 00х0 | х110 | 000х | хх01 | |||
| 1х10 |


 00х0
00х0
1х10



 00х0 000х А1 00х0
00х0 000х А1 00х0
1х10 х110 1х10
 А1 = х110 хх01 после выполнения 000х
А1 = х110 хх01 после выполнения 000х
000х С1= х010 Þ операцииÞС1= х110
хх01 0х10 поглошения хх01
0000 В1 х010
Z0=Ø 0х01 0х10
1х01
Среди кубов С0 возможно находятся такие кубы, которые с кубами множества А1 могут дать новые кубы, или оказаться простыми импликантами, после второго шага (С1*С1). При формировании таблицы для выполнения операции С1*С1 следует учесть, что В1*В1 уже выполнялось на шаге С0*С0. Следовательно:
С1*С1=(А1UВ1)*(А1UВ1)=(А1*А1)U(А1*В1)U(В1*А1)U(В1*В1)=(А1*А1)U(А1*В1)
Таблица 17.
| С1*С1 | 00х0 | 1х10 | 000х | х110 | хх01 | |
| 00х0 | - | |||||
| 1х10 | у010 | - | ||||
| 000х | ø | - | ||||
| х110 | 0у10 | ø | - | |||
| хх01 | 000у | ø | ø | - | ||
| х010 | 00у0 | ху10 | Ø | |||
| 0х10 | ух10 | 00у0 | Ø | |||
| А2 | ø | хх10 | ø | хх10 | Ø |
В результате выполнения умножения С1*С1 получено:
А2={хх1х}
|

 00х0
00х0
000х
Необходимо отметить, что куб хх01 не дал нового куба. Но это куб второй размерности и новые кубы может дать на третьем шаге (С3*С3). Поэтому его не следует включать в число кубов, образующих множество Z1.




 1х10 хх10
1х10 хх10

 х110 1х10
х110 1х10
|
|
х010 х010 хх01
0х10 0х10
хх01
Таблица 18.
| С2*С2 | хх10 | |
| хх10 | - | |
| хх01 | ø | |
| А3 | ø |
Таким образом, получено А3= Ø, следовательно, новых кубов нет.
|

 хх10
хх10
хх01
В3=С2-Z2= Ø; C3=A3UB3= Ø.
На этом процесс выявления простых импликант окончен.
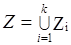

 00х0
00х0
|
хх01
хх10
Необходимо выяснить, не содержатся ли в этом множестве “лишние” импликанты.
2. Определение L-экстремалей.
Множество Z может быть избыточным. Прежде всего необходимо выявить обязательные простые импликанты, называемые в алгоритме извлечения L-экстремалями. L-экстремаль – это куб, который и только он покрывает некоторую вершину из множества L, не покрываемую никаким другим кубом из множества Z.
Для определения L-экстремалей воспользуемся операциями вычитания (#) и пересечения (∩) кубов.
Таблица 19.
| z#(Z-z) | 00x0 | 000x | xx01 | xx10 | |
| 00х0 | - | zzz1 | 11zy xx01 | 11zz 1x10 x110 | |
| 000х | zz1z | - | 11zz 1x01 x101 | y1yz 1x10 1yyz x110 | |
| xх01 | zzyy | zzzz ø | - | ||
| xх10 | zzzz ø | ø | zzyy 1x01 zzyy x101 | - | |
| остаток | Ø | Ø | 1x01 x101 | 1x10 x110 |
Таким образом из таблицы получено множество L-экстремалей.
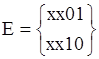
1. Если результат вычисления будет Ø хотя бы в одном, любом случае, то это значит, что среди простых импликант есть такие кубы, которые покрывают уменьшаемый, а следовательно этот уменьшаемый не может быть L-экстремалью.
2. Если же полученный результат не Ø, то в противоположность предыдущему утверждению уменьшаемый куб оказался кубом большей размерности по отношению к другим простым импликантам.
3. Что касается простых импликант, ”удаленных” от уменьшаемой, то они с ней дают координаты ”y” и таким образом остается уменьшаемый куб при вычитании этих ”удаленных” кубов.
После выявления L-экстремалей следует выяснить, не являются ли некоторые из них простыми импликантами, остатки которых покрывают только некоторое подмножество кубов комплекса N, которое нет необходимости покрывать, вводя в минимальное покрытие соответствующие наборы. Для этого необходимо выполнить операцию пересечения остатков, полученных при выполнении операции z#(Z-z) с кубами из комплекса L. Во множестве E необходимо оставить только те кубы, остатки от которых пересекаются с кубами из комплекса L.
Таблица 20.
| z#(Z-z)∩L | 1x01 | x101 | 1x10 | x110 | |
| x010 | ø | ø | ø | ||
| 0x10 | ø | ø | ø | ||
| ø | ø | ø | |||
| 0x01 | ø | ø | ø |
Из таблицы видно, что куб 1x01 не пересекается с кубами комплекса L. Однако куб x101 имеет с кубом 0x01 (из комплекса L) общую вершину 0101. Оба куба (1x01, x101) входят в куб более высокой размерности xx01 (L-экстремаль). Таким образом, куб 1x01, образованный на комплексе N, позволил уменьшить цену схемы. Выясним далее, какие из вершин комплекса L не покрываются L-экстремалями. Для этого из каждого куба комплекса L вычтем (#) элементы множества Е. В результате вычитания получим L1=L#Е.
Таблица 21.
| L#Е | x010 | 0x10 | 0x01 | ||
| xx01 | zzyy x010 | zzyy 0x10 | zzzy | zzzz ø | |
| xx10 | zzzz ø | zzzz ø | zzyz | ø | |
| ø | ø | ø |
Из таблицы видно, что L1={0000}. Однако непокрытые L-экстремалями кубы должны быть покрыты другими импликантами из множества.
Z=Z-E= 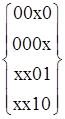
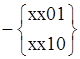
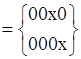
Теперь из полученного множества Z надо выбрать минимальное число кубов, с минимальной ценой (максимальной размерностью), чтобы покрыть непокрытые L-экстремалями элементы комплекса L. Выбор так называемого немаксимального куба осуществляется с помощью операции частичного упорядочивания кубов (<).
Куб a будет не максимален по отношению к кубу b, если выполняются одновременно два условия:
1) Сa ≥ Cb, где Са – цена куба а:;
2) a ∩ L1 Í b ∩ L1, куб b покрывает не меньше кубов чем куб а.
Z 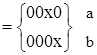
| Таблица 22. | ||||
| ∩ | ||||
| а | 00х0 | |||
| b | 000х |
Сa = Cb
Следовательно, кубы а и b равноценны и для покрытия вершины 0000 можно выбрать любой из них в качестве экстремали второго порядка
Е¢2={000x} или E¢¢2={00x0}.
Следовательно, могут быть получены две тупиковые формы.
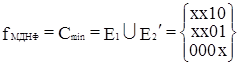 - первая тупиковая форма
- первая тупиковая форма
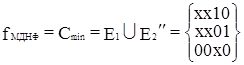 - вторая тупиковая форма
- вторая тупиковая форма
Дата добавления: 2015-05-05; просмотров: 1205;
