Метод Квайна
Теорема Квайна. Для получения минимальной формы логической функции необходимо в СДНФ произвести все возможные склеивания и поглощения так, что в результате будет получена сокращенная ДНФ. Сокращенная ДНФ в общем случае может содержать лишние простые импликанты, которые необходимо выявить на втором этапе минимизации.
На первом этапе выполняется переход от функции, заданной в форме СДНФ, к сокращенной ДНФ. Это основано на использовании следующих соотношений:
1. соотношение неполного склеивания:
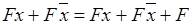 , где
, где 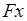 и
и 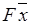 - две конъюнкции, а F - любое элементарное произведение;
- две конъюнкции, а F - любое элементарное произведение;
2. соотношение поглощения
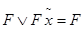 .
.
Справедливость обоих соотношений легко проверяется. Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к сокращенной ДНФ. Метод применим к совершенной ДНФ. Из соотношения поглощения следует, что произвольное элементарное произведение поглощается любой его частью. Для доказательства достаточно показать, что произвольная простая импликанта р = xi1xi2 ... xin может быть получена. В самом деле, применяя к р операцию развертывания (обратную операции склеивания):
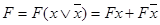
по всем недостающим переменным xik, ..., xim исходной функции f, получаем совокупность S конституент единицы. При склеивании всех конституент из S получим импликанту р. Последнее очевидно, поскольку операция склеивания обратна операции развертывания. Множество S конституент обязательно присутствует в совершенной ДНФ функции f поскольку р - ее импликанта.
В результате выполнения склеивания получается конъюнкция n-1 ранга, а конъюнкции 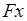 и
и 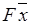 остаются в исходном выражении и участвуют в сравнении с другими членами СДНФ. Таким образом, удается снизить ранг термов.
остаются в исходном выражении и участвуют в сравнении с другими членами СДНФ. Таким образом, удается снизить ранг термов.
Склеивание и поглощение выполняются до тех пор, пока имеются члены, не участвовавшие в попарном сравнении. Термы, подвергшиеся операции склеивания, отмечаются. Неотмеченные термы представляют собой простые импликанты и включаются в сокращенную ДНФ. Все отмеченные конъюнкции ранга n-1 подвергаются вновь операции склеивания до получения термов n-2 ранга и так далее до тех пор, пока количество неотмеченных конъюнкций больше 2. В результате выполнения первого этапа получена сокращенная ДНФ.
Полученное логическое выражение не всегда оказывается минимальным. На втором этапе переходят от сокращенной ДНФ к тупиковым ДНФ и среди них выбирают МДНФ.
Для формирования тупиковых ДНФ строится импликантная таблица (матрица), строки которой отмечаются простыми импликантами сокращенной ДНФ, а столбцы конститутиентами единицы исходной СДНФ. В строке напротив каждой простой импликанты ставится метка под теми наборами (конститутиентами единицы), на которых она принимает значение 1. Соответствующие конститутиенты поглощаются (покрываются) данной простой импликантой.
Из общего числа простых импликант необходимо отобрать их минимальное число, исключив лишние. Формирование тупиковых форм и выбор минимального покрытия начинается с выявления обязательных простых импликант, то есть таких, которые (и только они) покрывают некоторый исходный набор. Рассмотрим на примере минимизации логической функции:





 fСДНФ= V (1,2,5,6,7)=x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3
fСДНФ= V (1,2,5,6,7)=x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3
1 2 3 4 5
Выполним операцию склеивания:
 1 – 3 (x1) x2x3 1
1 – 3 (x1) x2x3 1
 2 – 4 (x1) x2x3 2
2 – 4 (x1) x2x3 2
3 – 5 (x2) x1x3 3
4 – 5 (x3) x1x2 4
В результате выполнения первого шага склеивания получаем четыре новые конъюнкции, простых импликант не выявлено. Полученные конъюнкции более не склеиваются и образуют сокращенную ДНФ.

 fсокр СДНФ=x2x3+ x2x3+ x1x3+ x1x2
fсокр СДНФ=x2x3+ x2x3+ x1x3+ x1x2
Для выявления обязательных простых импликант и фрормирования на их основе минимального покрытия строится импликантная таблица (табл. 13). В строках импликантгой таблицы записываются простые импликанты, а в столбцах конституэнты единицы. Звездочка ставится если простая импликанта покрывает контитуэнту.
Таблица 13.
     
| x1x2x3 | X1x2x3 | x1x2x3 | x1x2x3 | x1x2x3 | ||

| x2x3 | * | * | ||||

| x2x3 | * | * | ||||
| x1x3 | * | * | |||||
| x1x2 | * | * |
Простые импликанты 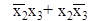 являются обязательными так как только они покрывают конституэнты
являются обязательными так как только они покрывают конституэнты 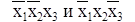 и включаются в минимальное покрытие. Остается одна непокрытая конституэнта x1x2x3 которая может быть покрыта одной из двух оставшихся простых импликант. Это приводит к получению двух тупиковых форм.
и включаются в минимальное покрытие. Остается одна непокрытая конституэнта x1x2x3 которая может быть покрыта одной из двух оставшихся простых импликант. Это приводит к получению двух тупиковых форм.
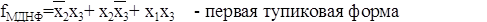
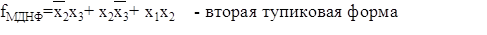
Дата добавления: 2015-05-05; просмотров: 1500;
