Материальной точки.

Основными понятиями релятивистской динамики, так же как и классической, являются масса и сила. До Эйнштейна инертная масса рассматривалась как величина постоянная. Но в 1901 г. физиками-экспериментаторами было обнаружено, что масса быстро движущихся электронов возрастает при увеличении скорости. Согласно теории относительности, масса одного и того же тела имеет различные значения в зависимости от скорости его движения и от выбора системы отсчета, в которой производится измерение. Зависимость массы m (движущегося относительно неподвижной системы отсчета) тела от скорости движения выражается соотношением: ,

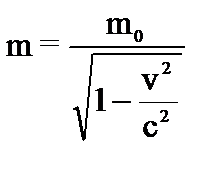где m₀ – масса покоя, т.е масса тела в системе отсчета, относительно которой оно покоится. Масса покоя есть инвариантная величина, одинаковая во всех системах отсчета. m называют релятивистской массой или массой движения.

При 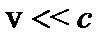релятивистская масса m стремится к m₀ (рис.25.1). Так же, как в классической, масса в релятивистской механике есть мера инертности, но инертность возрастает с ростом скорости, то есть чем больше скорость, тем «труднее» изменить эту скорость. При 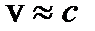инертность возрастает настолько, что дальнейшее увеличение скорости становится невозможным, поэтому скорость света предельна и недостижима.

Теория относительности не запрещает существования частиц, движущихся со скоростью света. Такими частицами являются фотоны, у которых масса покоя равна нулю.

В классической физике импульс определяется по формуле: 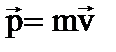. Но масса движущегося тела зависит от скорости, поэтому релятивистский импульс: 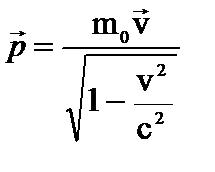. (1)

На рис.25.2. кривая 1 показывает зависимость релятивистского импульса от скорости тела, кривая 2 – классического импульса, определяемого по формуле: 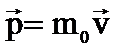. При малых скоростях графики совпадают. При скоростях движения, сравнимых со скоростью света, релятивистский и классический импульсы не совпадают. Значение релятивистского импульса стремится к бесконечности.

Для замкнутой системы и в релятивисткой динамике остается справедливым закон сохранения импульса.

Согласно первому постулату СТО все законы природы и их математическое описание должны быть инвариантны относительно инерциальных систем отсчета. Это же касается и законов динамики. Второй закон Ньютона: .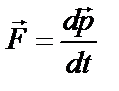

Это уравнение оказывается инвариантным, если относительно преобразований Лоренца, если производная по времени берется от релятивистского импульса (1): 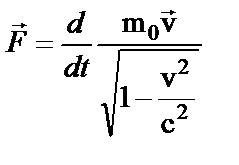(2)

Это основной закон релятивистской динамики материальной точки.Можно показать, что в отличие от классической механики, в релятивистской механике ускорение в общем случае не совпадает по направлению с вызывающей его силой. Только в двух случаях вектор ускорения коллинеарен вектору силы:

а) 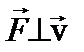– на материальную точку действует поперечная сила, которая вызывает изменение скорости только по направлению, а модуль скорости и релятивистская масса не изменяются:

б) 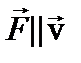– на материальную точку действует продольная сила, которая вызывает изменение модуля скорости и массы материальной точки.

Причем поперечная сила сообщает материальной точке большее ускорение, чем равная по модулю продольная сила.