Момент силы. Момент инерции.
Теперь мы будем рассматривать движение такого тела, при котором существенную роль играют его размеры и форма, и поэтому тело нельзя рассматривать как материальную точку.
Введем основные величины применительно к простому случаю вращения твердого тела вокруг неподвижной оси. Пусть внешние силы, приложенные к разным точкам тела, лежат в плоскостях, перпендикулярных оси вращения. Будем считать, что при вращении трение пренебрежимо мало. Разобьем тело на столь малые элементы, чтобы их можно было бы считать материальными точками. Пусть на i-ю материальную точку массой mi и радиуса-вектора 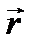 , действует внешняя сила
, действует внешняя сила 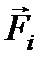 под углом
под углом  к направлению радиуса вектора (рис.14.1). Величина, равная векторному произведению радиуса-вектора материальной точки на вектор силы, называется моментом силы относительно заданной оси вращения:
к направлению радиуса вектора (рис.14.1). Величина, равная векторному произведению радиуса-вектора материальной точки на вектор силы, называется моментом силы относительно заданной оси вращения:
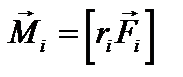 (1).
(1).
 Вектор
Вектор 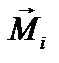 направлен вдоль оси вращения. С помощью правила буравчика определяют, в какую именно сторону вдоль оси он направлен. Размерность [M]=Н.м.
направлен вдоль оси вращения. С помощью правила буравчика определяют, в какую именно сторону вдоль оси он направлен. Размерность [M]=Н.м.
Из (1) вытекает, что 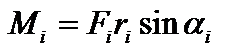 . Продолжим линию силы и найдем плечо силы
. Продолжим линию силы и найдем плечо силы 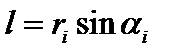 , тогда модуль момента силы:
, тогда модуль момента силы: 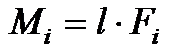 . определяется как произведение силы на плечо.
. определяется как произведение силы на плечо.
Если внешние силы приложены к нескольким точкам тела, то результирующий или полный момент относительно оси вращения равен алгебраической сумме моментов каждой из сил относительной той же оси. 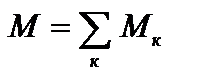 . Например, на (рис.14.2) результирующий момент: М=М1–М2 + М3.
. Например, на (рис.14.2) результирующий момент: М=М1–М2 + М3.
Введем определение момента инерции тела относительно данной оси вращения. Момент инерции тела относительно оси вращения определяется как сумма моментов инерции материальных точек, составляющих тело.
Момент инерции материальной точки mi определяется как величина, численно равная произведению массы на квадрат расстояния точки до оси вращения: 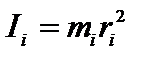 .
.
Тогда момент инерции тела: 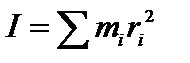 .
.
В общем случае, если тело сплошное, оно представляет собой множество точек с бесконечно малыми массам 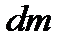 , и момент инерции тела определяется интегралом. Пределы интегрирования определяются размерами и формой тела:
, и момент инерции тела определяется интегралом. Пределы интегрирования определяются размерами и формой тела:
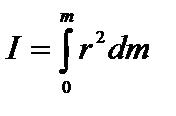 .
.
Момент инерции зависит от формы тела, относительно какой оси вращается тело, от распределения массы по объему тела. В таблице приведены моменты инерции некоторых тел правильной геометрической формы:
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
| Однородный тонкий стержень массой m и длиной l | Проходит через центр тяжести стержня перпендикулярно стержню Проходит через конец стержня перпендикулярно стержню | 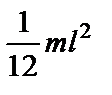
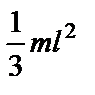
|
| Тонкие кольцо, обруч, труба радиусом R и массой m, распределенной по ободу | Проходит через центр перпендикулярно плоскости основания | mR2 |
| Круглый однородный диск (цилиндр) радиусом R и массой m | Проходит через центр диска перпендикулярно Проходит через центр плоскости основания | 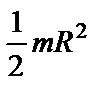
|
| Однородный шар массой m и радиусом R | Проходит через центр шара |
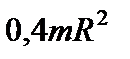
|
Если ось вращения перенести на другое расстояние, то момент инерции изменяется и определяется с помощью теоремы Штейнера: момент инерции тела  относительно произвольной оси равен моменту инерции
относительно произвольной оси равен моменту инерции 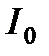 относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния d между осями:
относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния d между осями:
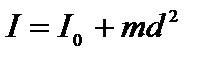
Дата добавления: 2015-04-01; просмотров: 2338;
