Закон сохранения механической энергии в консервативнойсистеме.

Пусть имеем систему материальных точек. Относительно системы отсчета координаты точки изменяются вследствие их движения. Кроме того, они взаимодействуют между собой: Е_К+Е_Р=Е

Сумма потенциальной и кинетической энергии всех точек, входящих в эту систему, называется полной.

Выясним, как изменяется энергия в консервативной системе. Для этого запишем уравнение движения для i-ой точки:

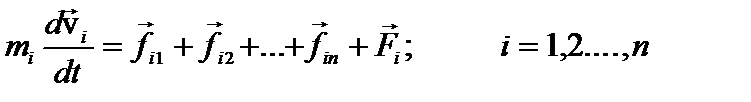
где 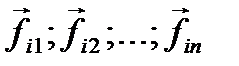– внутренние силы, действующие на i-ю точку, 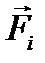–внешние.

За малое время dt точка совершит перемещение 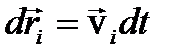. Умножим это выражение с уравнением движения:

.

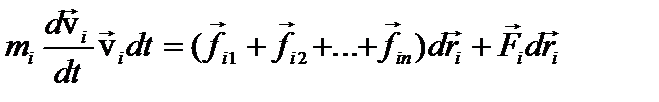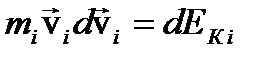– изменение кинетической энергии одной точки.

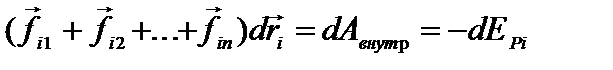– изменение ее потенциальной энергии.

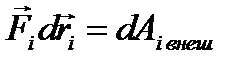– работа внешних сил.

В итоге получаем: .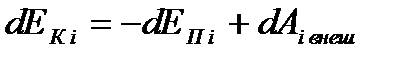

Просуммируем левые и правые части по всем точкам:

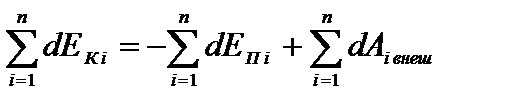Þ

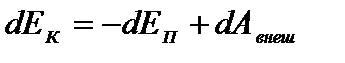
dE_К–изменение кинетической энергии всех точек,

dE_Р– изменение потенциальной энергии всех точек,

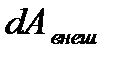–работа внешних сил над всей системой за время dt.

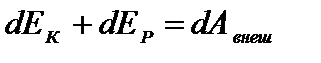Þ .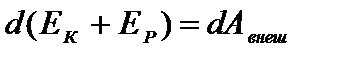

Но 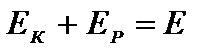– полная механическая энергия системы.

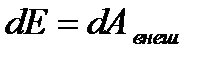
dE – изменение полной механической энергии за время dt. Проинтегрируем по всему промежутку времени от t₁ до t₂.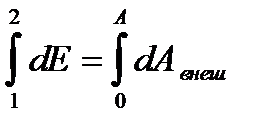

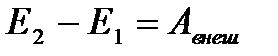
Изменение полной механической энергии в незамкнутой консервативной системе равна работе внешних сил.

Если консервативная система замкнута, то внешние силы отсутствуют:

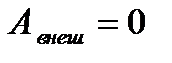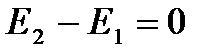Þ Þ 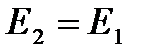E = const.

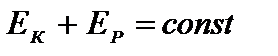
закон сохранения замкнутой консервативной системы: