Закон сохранения импульса.
Третий закон Ньютона в соединении с первым и вторым законами позволили перейти от динамики отдельной материальной точки к динамике произвольной механической системы. Рассмотрим механическую систему, состоящую из n материальных точек. Для i-й материальной точки согласно второму закону Ньютона: 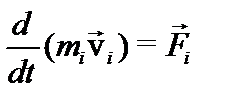 . (1)
. (1)
Все тела, не входящие в рассматриваемую механическую систему , называются внешними, а силы, действующие со стороны этих тел, называются внешними силами. Силы взаимодействия частей самой системы называются внутренними.
Пусть 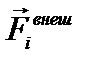 – сумма всех внешних сил, действующих на i-ю точку системы,
– сумма всех внешних сил, действующих на i-ю точку системы, 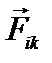 – внутренняя сила, действующая на i-ю точку со стороны k-ой, тогда:
– внутренняя сила, действующая на i-ю точку со стороны k-ой, тогда: 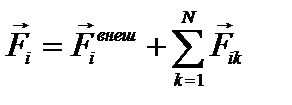 . В результате (1) примет вид:
. В результате (1) примет вид:
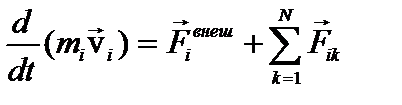 (2)
(2)
Просуммируем левые и правые части (2) по i для всех материальных точек:
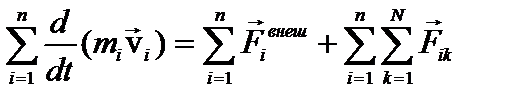 (3)
(3)
По третьему закону Ньютона: 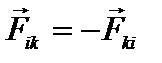 . Отсюда
. Отсюда 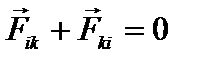 , т.е.
, т.е.
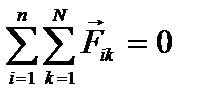 .
.
Обозначим: 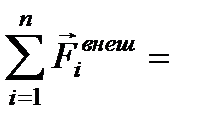
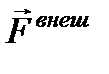 – результирующая всех внешних сил и
– результирующая всех внешних сил и 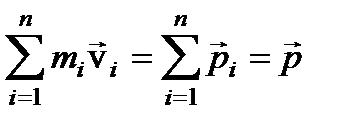 – импульс механической системы. Отсюда (3) примет вид:
– импульс механической системы. Отсюда (3) примет вид: 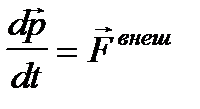 (4)
(4)
Мы получили закон изменения импульса механической системы: производная по времени от импульса механической системы равна вектору внешних сил, действующих на систему.
Рассмотрим замкнутую (или изолированную) систему. Механическая система, на которую не действуют внешние силы, называют замкнутой системой.
Итак, если система замкнута, то 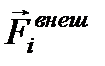 = 0. Из закона динамики для системы тел (материальных точек):
= 0. Из закона динамики для системы тел (материальных точек): 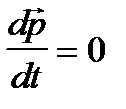 (5)
(5)
Из (5) следует, что 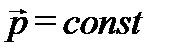 или
или 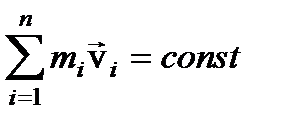 (6)
(6)
Мы пришли к закону сохранения полного импульса изолированной системы: при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным.
Закон сохранения полного импульса изолированной системы – это универсальный закон природы. В более общем случае, когда система незамкнута, из (4) следует, что полный импульс незамкнутой системы не остается постоянным. Его изменение за единицу времени равно геометрической сумме всех внешних сил.
Если система незамкнута, то полный импульс незамкнутой системы не остается постоянным. Его изменение за единицу времени равно геометрической сумме всех внешних сил. Однако в некоторых случаях импульс незамкнутой системы также может сохраняться:
а) Иногда (например, при взрыве, ударе или выстреле) импульсы частей системы претерпевают большие изменения за сравнительно короткие промежутки времени. Это связано с возникновением в системе кратковременных, но весьма значительных по величине внутренних сил взаимодействия частей системы, по сравнению с которыми все постоянно действующие на систему внешние силы оказываются малыми. В этом случае внешними силами мы пренебрегаем, и импульс всей системы в целом не изменяется.
б) Если система не замкнута, но 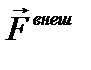 = 0, то по закону сохранения импульса импульс системы не изменяется с течением времени:
= 0, то по закону сохранения импульса импульс системы не изменяется с течением времени: 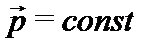 .
.
в) Может оказаться, 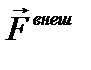 ¹ 0, и
¹ 0, и 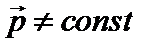 , но
, но 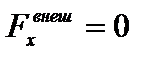 или
или 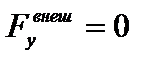 . Тогда
. Тогда 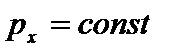 или
или 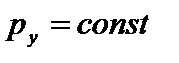 . Например, на систему действуют внешние силы, направленные вертикально, тогда
. Например, на систему действуют внешние силы, направленные вертикально, тогда 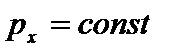 .
.
Дата добавления: 2015-04-01; просмотров: 1337;
