Соударение двух тел.

Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.

Удар или соударение – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. При рассмотрении столкновений необходимо знать форму тел, массы покоя, скорости движения и их упругие свойства. Простейшим видом соударений является центральный удар тел, при котором тела до удара движутся поступательно вдоль прямой, проходящей через их центры масс.

Существует два предельных вида удара: абсолютно упругий и абсолютно неупругий. Рассмотрим центральный удар шаров для этих видов удара.

1. Абсолютно неупругий удар – это такой удар, после которого скорость соударяющихся тел оказывается одинаковой (рис.13.1).

При абсолютно неупругом ударе кинетическая энергия тел полностью или частично превращается во внутреннюю энергию, поэтому здесь неприменим закон сохранения механической энергии, а применим лишь закон сохранения импульса: 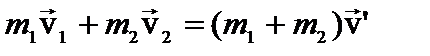, Þ .

Частным случаем рассматриваемого взаимодействия будет такой, когда первоначальные импульсы 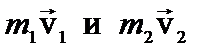тел будут равны по модулю, но противоположны по направлению. В этом случае кинетическая энергия взаимодействующих тел полностью переходит во внутреннюю энергию, так как при этом совершается работа по деформации тел.

В общем случае во внутреннюю энергию тел переходит часть кинетической энергии (идет на работу деформации и нагревание тел), величину которой можно определить по разности кинетической энергии тел до и после удара:

.

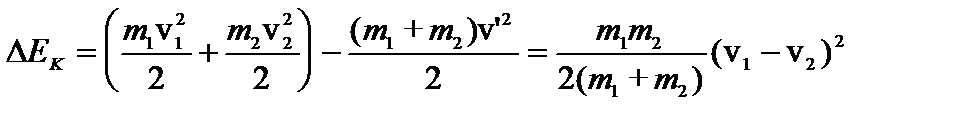Таким образом, для неупругого удара не выполняется закон сохранения механической энергии, но справедлив сохранения закон суммарной энергии различных видов – механической и внутренней.

2. Абсолютно упругийудар–это такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии, так как этом случае нет деформации, на которую бы расходовалась часть энергии. Следовательно, для абсолютно упругого удара выполняются законы сохранения механической энергии и импульса:

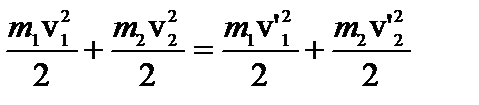
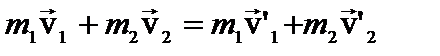
Перепишем систему в виде: 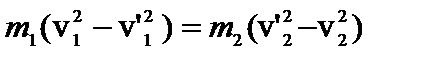(1)

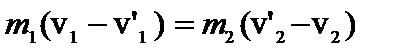(2)

Полагая 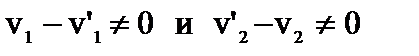, поделим первое уравнение на второе: (3)

Решая систему из уравнений (3) и (2), получаем:

; .

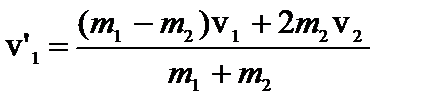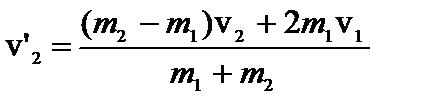Скорости имеют положительный знак, если они совпадают с положительным направлением оси, выбранной нами, и отрицательный – в противном случае.

Проанализируем полученные выражения для двух шаров различных масс.

1. 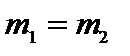. Þ ; .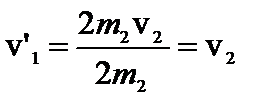

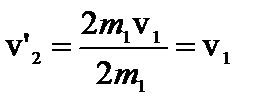Шары равной массы «обмениваются» скоростями.

2. , ,

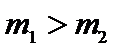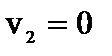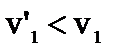, следовательно, первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью;