Определение констант равновесия. Тепловая теорема Нернста
Формула (17.17) дает возможность определять значения констант равновесия для любых температур. В интегральном виде эта формула имеет вид
.
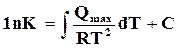Для использования в вычислениях этой формулы необходимо определить значение константы С. Это значение может быть получено, если экспериментально определены для какой-нибудь температуры значения К и тепловой эффект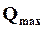 
. Подсчитанное значение Сподставляется в формулу, после чего она может быть использована для вычисления К при любых температурах.
Имеется другой путь нахождения значения К, путь чисто аналитический, основанный на тепловой теоремеНернста, называемой третьим законом термодинамики.
Нернст, используя большой экспериментальный материал, накопленный при изучении поведения конденсированных (твердых и жидких) веществ, при низких температурах, установил, что разность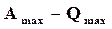 
мала и с понижением температуры до абсолютного нуля уменьшается быстрее, чем по линейному закону. Из выражения (16.48) при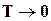 
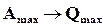, но 
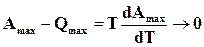, поэтому
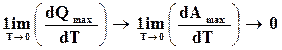(17.19)
Эти уравнения дают возможность исключить константу интегрирования и получить зависимость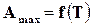 
аналитическим путем. Уравнение (17.19) математически выражает тепловую теорему Нернста. На основе этой теоремы можно утверждать, что в уравнении Кирхгофа (16.15) при 0 К разность теплоемкостей в правой части стремиться к нулю, следовательно, и сами теплоемкости конденсированных систем также стремятся к нулю.
Планк, основываясь на теореме Нернста, пришел к дополнительным выводам относительно энтропии.
Из уравнения (16.44) можно записать
.
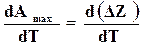В соответствии с уравнением (16.33)
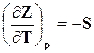, следовательно,
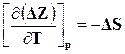и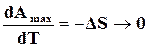 
. (17.20)
На основании зависимостей (17.20) следует, что вблизи 0 К все реакции происходят без изменения энтропии, а при 0 К сама энтропия конденсированных систем равна нулю, т. е.
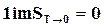и в начале отсчета S0=0. (17.21)
Из уравнения (17.21) следует, что приТ=0 К, когда отсутствует тепловое движение, энтропия конденсированной системы равна нулю. Это происходит вследствие того, что при приближении к абсолютному нулю значительно уменьшается термодинамическая вероятность, и одновременно упорядочивается взаимное расположение молекул. Образуется периодическая пространственная решетка, в которой каждая молекула неподвижна. Таким образом, при абсолютном нуле равновесия система находится в состоянии, когда термодинамическая вероятность такого состояния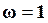 
.
Поэтому по формуле Больцмана
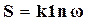получаем, что при Т=0 энтропия S=0.
Следовательно, при приближении к абсолютному нулю энтропия каждого однородного кристаллического тела неограниченно стремиться к нулю. Это положение представляет собой третий закон термодинамики в формулировке Планка.
Положение третьего закона термодинамики позволяют определить значение константы интегрирования для вычисления абсолютного значения энтропии. Используя дифференциальные уравнения термодинамики, можно также определить абсолютные значения основных термодинамических функций F, Z и д. р.
Дата добавления: 2015-04-03; просмотров: 1792;