Пример построения пороговых схем в пакете Multisim
Пороговой схемой L из M (L/M) называют комбинационную схему, имеющую m входов и один выход y и реализующую y=1 только в тех случаях, когда не менее L входных сигналов равны единице.
Для обнаружения по критерию L/M потребуется M!/[L!(M-L)!]+1 логических элемента в базисе И-НЕ. Рассмотрим способ определения числа единиц на m позициях. Если это число единиц не менее L, применяется решение об обнаружении (y=1). Применение сумматоров для определения числа единиц позволяет существенно упростить расчетную часть и предельно снизить элементные затраты. Так как все входные переменные имеют одинаковый вес (единицу), то для их сложения с целью последующего сравнения пороговым числом L потребуются одноразрядные сумматоры.
Алгоритм построения ПС будет заключаться в следующем:
1) строится сумматор для сложения M единиц;
2) строится КС, позволяющая выявить (дешифрировать) требуемое число L на выходе построенного сумматора (если оно выявляется, то на выходе схемы должна быть единица).
Приведем пример синтеза пороговой схемы (6/9). На рис. 6.1 показана эта схема, реализованная на 6 одноразрядных сумматорах и одном ЛЭ ИЛИ. Если на вход сумматора подается переменная, имеющая вес 2m , то выход суммы имеет также вес 2m , а перенос – вес 2m+1. На все три входа сумматора можно подавать только переменные, имеющие одинаковые веса. С помощью сумматоров SM1-SM5 производится обычное сложение двоичных чисел. Выходными сигналами этой части являются сигналы yj, j=0,1,2,3. Так как L=6 – четное число, то переменная y0, имеющая вес 1, не может оказать влияние на превышение суммой переменных xM (m=1,2,3,4,5,6,7,8,9) порога L, т.е. эту переменную можно исключить из дальнейшего рассмотрения. Таким образом, остались три переменные: y1 - переменная, имеющая вес 4, и переменные y2 и y3 имеющие вес 2.
Очевидно, что порог L=6 будет превышен только в 2-х случаях:
1) если y1=1 и y2=1,
2) y1 и y3=1.
Поэтому для окончательного построения пороговой схемы надо реализовать функцию f(v)=y1y2 Ú y1y3. Для реализации этой функции можно использовать сумматор SM6. Так как P1=A1B1 Ú A1P0 Ú B1P0 и S=A1 Å B1 Å P0, то, положив A1=y1, B1= y2 Ú y3 и P0=0, получим, что f(v)=P1. Аналогичным образом можно реализовать любую пороговую схему при сколь угодно большом числе входных сигналов n.
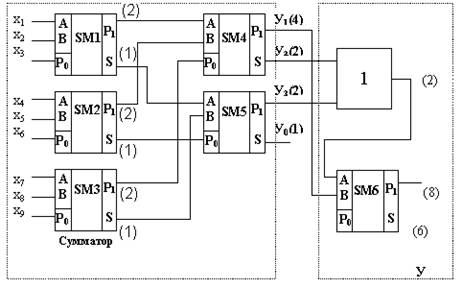
Рис. 6.1 Пороговая схема 6/9
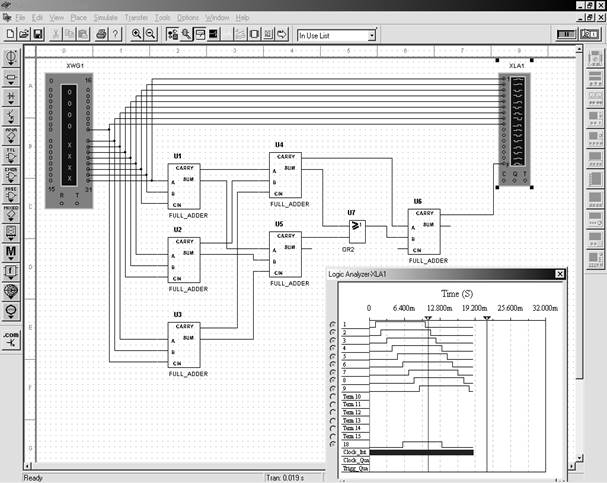
Рис. 6.2 Пороговая схема 6/9 с временными диаграммами
При построении ПС с условием 5/9 на одноразрядных сумматорах необходимо построить сумматор для сложения 9 единиц (рис. 6.3). На выходе схемы сложения необходимо построить КС, срабатывающую при условии L >= 5. Для этого необходимо просуммировать старший разряд с выхода сумматора, вес которого равен 4, с остальными выходами, объединенными по схеме ИЛИ. Если каждый из этих двух сигналов будет равен единице, то, сложив их на выходе переноса, получим требуемое значение, т.е. на выходе схемы будет высокий уровень, при L >= 5 и низкий уровень, при L < 5.
Схема сумматора должна иметь столько выходов, чтобы можно было закодировать число М. В рассматриваемом примере М = 9, значит, сумматор должен иметь 4 выхода. Для выполнения этого условия необходимо взять 5 одноразрядных сумматоров, где выход переполнения схемы сумматора является старшим разрядом дешифрируемого числа L, т.е. имеет вес = 4. Далее нам необходимо построить КС чтобы выявить число L = 5.
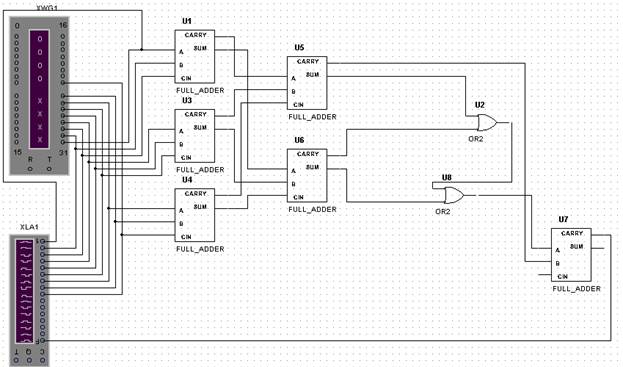
Рис. 6.3 Пороговая схема на одноразрядных полных сумматорах (5/9)
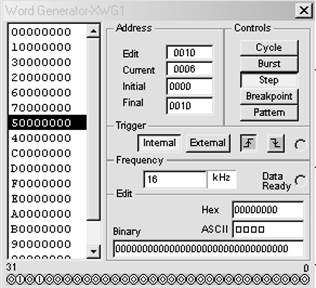
Рис. 6.4 Заданная последовательность сигналов для схемы 5/9 (см. рис. 6.3)
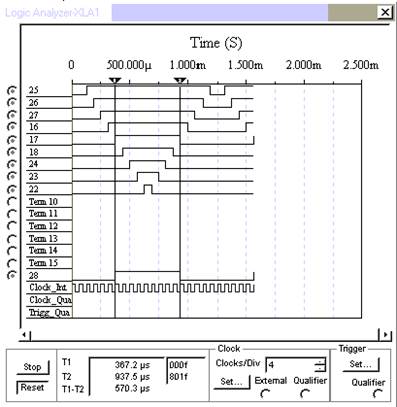
Рис. 6.5 Временные диаграммы для схемы 5/9 (см. рис. 6.3)
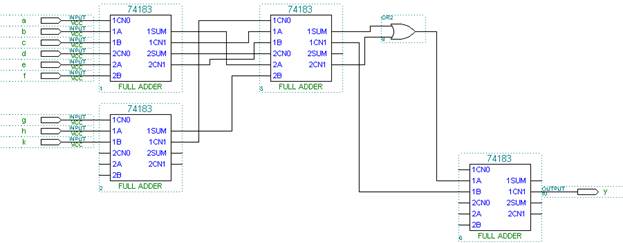
Рис. 6.6 Пороговая схема 5/9 в пакете MAX+Plus II
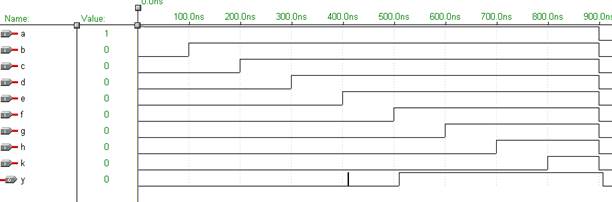
Рис. 6.7 Временные диаграммы для схемы 5/9
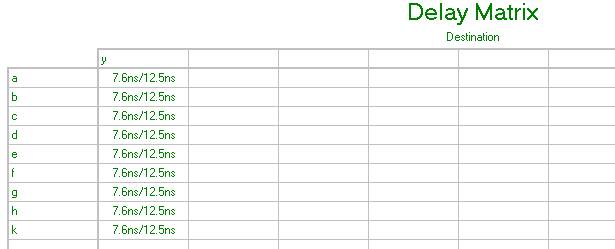
Рис. 6.8 Матрица временных задержек
Программа:
TITLE "porogovay_shema_5_9";
SUBDESIGN porogovay_shema_5_9
(
a, b, c, d, e, f, g, h, k: INPUT;
y : OUTPUT;
)
VARIABLE z : NODE;
BEGIN
z = a + b + c + d + e + f + g + h + k;
IF z>=5 THEN
y = VCC;
ELSE
y = GND;
END IF;
END;
Дата добавления: 2015-04-25; просмотров: 3952;
