Прямой, обратный и дополнительный коды

Для выполнения в ЭВМ арифметических операций необходимо использовать специальное кодирование отрицательных чисел. Для представления знака числа требуется введение дополнительного знакового разряда. Знак минус принято кодировать символом «1», а знак плюс – символом «0».

Прямой код. Прямой код целого n-разрядного двоичного числа 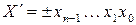задается соотношением:

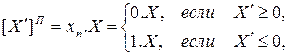
где 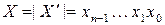– модуль числа 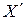, а прямой код 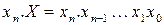(для наглядности знаковый разряд отделяется точкой). Числу 0 может быть приписан любой знак. Таким образом, прямой код числа 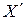произвольного знака получается добавлением к модулю числа 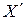знакового разряда 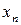, значение которого и определяет знак числа.

То есть, имеем: знаковый разряд располагается слева от числа и отделяется от последнего точкой, например: +5 = 0.101;-5=1.101.

Прямой код упрощает умножение чисел, так как в этом случае для вычисления произведения необходимо перемножить модули чисел 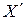и и 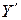вычислить знак произведения 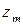, который определяется только значениями знаков чисел 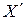и 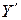. Знак произведения 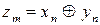, где .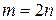

Обратный код. Обратный код целого n-разрядного двоичного числа 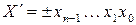определяется соотношением:

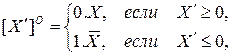
где 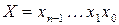– модуль числа ,

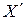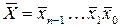
Число 0 в обратном коде имеет два представления: 0.0…00 – положительный и 1.1…11 – отрицательный нули. В (n+1)-разрядных (с учетом знакового разряда) прямом и обратном кодах могут быть представлены числа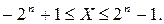

То есть, имеем: обратный код двоичного отрицательного числа получается из прямого кода равного ему положительного числа инвертированием значений всех его разрядов. Например, обратный код числа -5₁₀=1.1012 есть 1.010.

Дополнительный код. Пусть требуется найти разность двух целых положительных n-разрядных чисел:

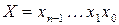и ,

где , .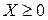

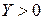Так как разность 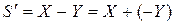, то вычитание эквивалентно сложению с отрицательным числом 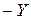. В двоичной системе счисления:

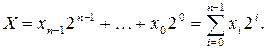
Максимальное значение X получается при 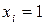для всех :

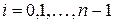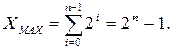(6.2)

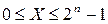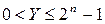Таким образом, и . Разность

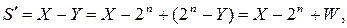(6.3)

где 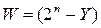. Так как значения 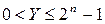, то 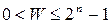. Положительное число 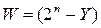на­зывается дополнением Y до 2ⁿ. Из соотношения (6.3) следует, что 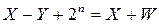, т. е. вычитание сводится к сложению, но результат надо скорректировать на 2ⁿ (вычесть из разности число 2ⁿ). Из выражения (6.2) следует, что

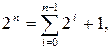
поэтому

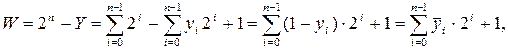
так как 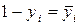. Поскольку 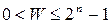, то

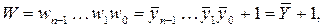
где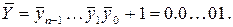

Разность (6.3) можно представить в виде:

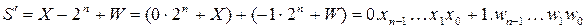(6.4)

где ,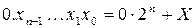

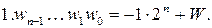
Величина 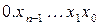называется дополнительным кодом положительного числа X (совпадает с пря­мым кодом), а величина – дополнительным кодом отрицательного числа -Y. Здесь значение n-го разряда определяет знак числа (0 – число положительное, 1 – число отрицательное). Из (6.4) следует, что знаковый разряд имеет вес -2ⁿ.

Если число Y может иметь любой знак, то дополнительный код

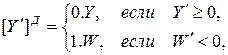(6.5)

где , .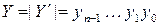

Из определения (6.5) следуют правила получения дополнительного кода отрицательных чисел (пра­вила преобразования прямого кода в дополнительный). Для этого необходимо: записать модуль 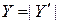отрицательного числа 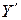в двоичной системе счисления; взять инверсию от каждого разряда числа, т.е. вычислить число 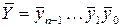; сложить полученное число 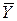с единицей, т.е. вычислить число 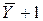; записать 1 в n-й разряд.