Общие принципы синтеза алгоритмической структуры системы управления
Для решения задачи синтеза алгоритмической структуры должны быть известны передаточная функция Wo(p) объекта управления, возмущения хв, действующие на входе и выходе объекта, а также помехи, возникающие в каналах задания и измерения (рисунок 9.15, а, б).
В простейшем случае, когда возмущающие воздействия на объект отсутствуют, управление можно осуществлять по разомкнутой схеме (рисунок 9.15, а). Если при этом передаточную функцию Wу(р) управляющего устройства принять равной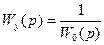 
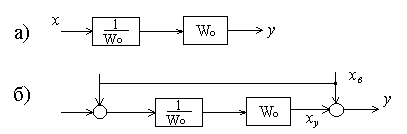
Рисунок 9.15 Простейшая структурная оптимизация САУ (а – при отсутствии возмущений, б – с возможностью полной компенсации возмущения)
то обеспечится полная (структурная) компенсация инерционности объекта, и система управления будет практически мгновенно воспроизводить на выходе объекта задающее воздействие.
Если на объект действует возмущение хв, которое поддается измерению, то теоретически можно синтезировать идеальную разомкнутую систему управления с полной компенсацией возмущения (рисунок 9.15, б). Причем, передаточная функция, обеспечивающая полную компенсацию инерционности объекта, оказывается наилучшей и для компенсации возмущения хв. Действительно, при выполнении условия
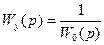(9.27)
всегда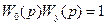 
, поэтому полезная составляющая хy на выходе объекта будет полностью уравновешивать возмущение хв.
Однако, возмущение хв как правило, не удается измерить, и систему управления приходится строить по замкнутой схеме или по принципу обратной связи. Для отыскания структуры идеальной замкнутой системы можно использовать идею косвенного измерения возмущения хв с помощью модели объекта Woм(p) (рисунок 9.16, а). Очевидно, что при:
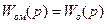, (9.28)
вычисляемый на выходе модели (см. штриховые стрелки) сигнал
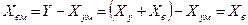, (9.29)
является косвенно измеренным возмущением хв, и его можно, как и в предыдущей схеме (рисунок 9.16, б), ввести в управляющее устройство с передаточной функцией 1/Wo(р) и, таким образом, снова получить идеальную разомкнутую структуру. В ней, в соответствии с правилами структурных преобразований, сигнал хум можно перенести на вход управляющего устройства и приложить к сумматору 2. Тогда управляющее устройство 1/Wо, окажется охваченным внутренней положительной обратной связью, а сигнал после сумматора 1 будет соответствовать сигналу ошибки. Последнее означает, что система стала замкнутой и работает по принципу отрицательной обратной связи с регулятором (рисунок 9.16, а, штриховой прямоугольник).
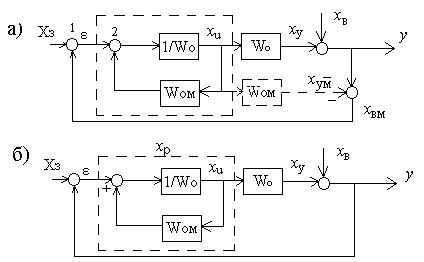
Рисунок 9.16 САУ с косвенным измерением возмущающего воздействия с использованием модели объекта управления
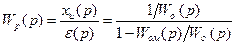. (9.30)
При точном совпадении модели и объекта регулятор Wp(p) будет работать как пропорциональный с кp=¥, что соответствует нулевым ошибкам по каналам задания и возмущения.
Используемое в идеальной системе включение последовательно с объектом звена в виде обратной модели объекта является принципиальной основой структурного и параметрического синтеза систем управления, а сам прием называется методом компенсации инерционности объекта.
В практических задачах синтеза чаще всего применяется частичная (параметрическая) компенсация – устранение влияния одной – двух (обычно самых больших) постоянных времени объекта. Для этого последовательно с инерционным объектом:
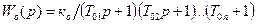, (9.31)
где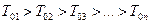 
, включают форсирующее звено первого – второго порядка с передаточной функцией:
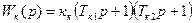, (9.32)
для которого постоянные времени должны быть равны компенсируемым постоянным времени объекта, т. е.:
; 
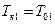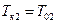
и передаточный коэффициент:
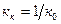
Следует заметить, что практическая реализация систем с идеальной структурой (рисунок 9.16, б) и применение метода компенсации инерционности объекта связаны с определенными техническими ограничениями и препятствиями, которые не всегда могут быть преодолены. В частности: как правило, невозможно точно реализовать обратную передаточную функцию объекта 1/Wo. Форсирующие звенья (9.32), используемые для частичной компенсации инерционности объекта, реально имеют свою инерционность. Регулятор с внутренней положительной обратной связью обычно структурно неустойчив или имеет большой передаточный коэффициент, который вызывает нереализуемые управляющие воздействия. Тем не менее, несмотря на невозможность практической реализации системы с идеальной структурой, она является теоретическим пределом, к которому необходимо стремиться при синтезе высококачественных систем управления. Таким образом, принцип структурно – параметрической оптимизации систем управления с обратной связью можно сформулировать следующим образом: управляющее устройство должно содержать динамическое звено с передаточной функцией, равной или близкой обратной передаточной функции объекта.
Установить степень приближения к желаемому теоретическому пределу возможно путём использования различных критериев.
При проектировании систем управления объектами, не содержащими чистого запаздывания, наибольшее применение получили два критерия – модульный оптимум (МО) и симметричный оптимум (СО).
Критерий модульного оптимума, называемый также критерием амплитудного или технического оптимума, заключается в выполнении следующих требований к форме амплитудной характеристики A(v), замкнутой системы по каналу хз … y: характеристика в как можно более широком диапазоне частот должна быть горизонтальной и равной единице; наклонный участок характеристики должен быть как можно более крутопадающим. Другими словами, критерий модульного оптимума требует, чтобы настраиваемая система приближалась по своим частотным передаточным свойствам к идеальному фильтру низкой частоты, имеющему, как известно прямоугольную частотную характеристику с частотой пропускания равной резонансной частоте vпр = vо. Тогда при отсутствии помехи на входе, система будет наилучшим образом воспроизводить задающее воздействие хз, и подавлять возмущение хв. При наличии на входе высокочастотной помехи частоту пропускания vп, системы выбирают также достаточно большой, но по компромиссному условию совместной фильтрации всех действующих сигналов.
Амплитудную характеристику, близкую по форме к прямоугольной характеристике идеального фильтра, имеет так называемый фильтр Баттерворта, у которого АЧХ:
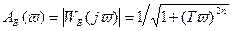, (9.33)
На практике обычно используют фильтры с порядком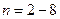 
. Нетрудно убедиться, что колебательная модель:
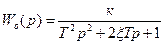, (9.34)
замкнутой системы при коэффициенте демпфирования x = 0,7 имеет амплитудную характеристику:
,
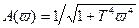соответствующую частному случаю фильтра с n = 2.
Таким образом, в рамках приближенной модели критерию МО соответствует значение коэффициента демпфирования x = 0,7; при этом главные показатели качества:
; 
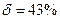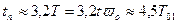(9.35)
где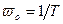 
– частота собственных незатухающих колебаний замкнутой системы (при x=0), характеризующая полосу пропускания фильтра; T01 – постоянная времени разомкнутого контура системы.
Для колебательной модели нестрогий критерий МО обеспечивает одновременно минимумы интегральной и «улучшенной» интегральных оценок с весовым коэффициентом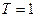 
.
Настройку на модульный оптимум применяют для контуров регулирования при передаточной функции объекта
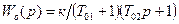, (9.36)
Здесь T01 является наименьшей постоянной времени, влияние которой не компенсируется, причем Т01 приближенно заменяет собой несколько постоянных времени с еще более малыми значениями Тoi т.е.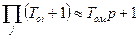 
и 
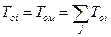
Регулятор в данном случае имеет передаточную функцию:
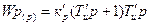, (9.37)
где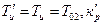 
соответствующей передаточной функции ПИ-регулятора.
Передаточная функция разомкнутой системы будет иметь вид
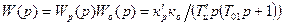, (9.38)
Очевидно, что при единичной обратной связи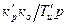 
.
На рисунке 9.17, а показаны ЛАЧХ L(v) разомкнутого контура и переходная характеристика h(t) замкнутой системы с объектом (9.36) и ПИ-регулятором, настроенным на МО. Передаточная функция замкнутого контура, настроенного на МО, имеет вид:
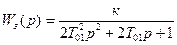, (9.39)
Ей соответствуют показатели качества:
, 
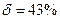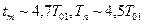
При необходимости реализовать астатическое регулирование в данном случае пользуются настройкой на симметричный оптимум (СО).
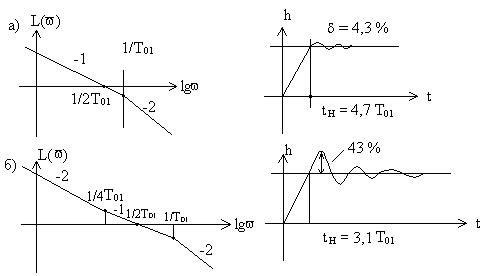
Рисунок 9.17 Частотные и переходные характеристики одноконтурной системы регулирования, настроенной по критериям модульного (а) и симметричного (б) оптимумов
Для астатических объектов второго порядка вида:
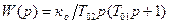, (9.40)
по условиям структурной устойчивости замкнутой системы нельзя использовать ПИ-регулятор с настройкой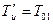 
, полностью компенсирующей единственную постоянную времени. Поэтому для таких объектов применяют настройку 
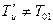, обеспечивающую лишь частичную компенсацию постоянной времени Т01. Найдем наилучшие соотношения настроечных параметров для частичной компенсации. Передаточная функция разомкнутого контура, состоящего из астатического объекта (9.40) и ПИ-регулятора с 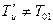, имеет вид:
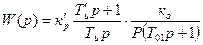, (9.41)
Ей соответствует передаточная функция замкнутой системы:
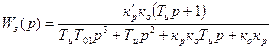, (9.42)
Применяя к знаменателю функции (9.42) соотношения Баттерворта, можно получить следующие настройки ПИ-регулятора:
; 
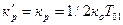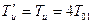= Tи = 4T01
причем Ти = 2Т01.
При полученных настройках передаточные функции (9.41) и (9.42) принимают вид:
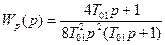, (9.43)
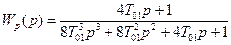, (9.44)
Передаточной функции (9.43) соответствует симметричная ЛАЧХ (рисунок 9.17, б), поэтому изложенный подход к выбору настроек получил название симметричного оптимума.
Передаточной функции (9.44) соответствует переходная характеристика замкнутой системы (рисунок 9.17, б). Переходный процесс в контуре, настроенном на СО, характеризуется следующими показателями:
, 
; 
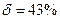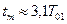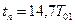
Для сравнения передаточных свойств контуров, настроенных по разным критериям, найдем передаточные функции замкнутой системы по каналу хв:
а) по критерию МО:
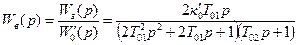, (9.45)
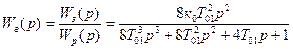, (9.46)
где Wз(р) – передаточные функции замкнутой системы по основному каналу.
Сравнивая попарно функции (9.39 и 9.44) и (9.45 и 9.46), обратим внимание на следующие их особенности и различия. Все функции имеют знаменатели, соответствующие полиномам Баттерворта. Это означает, что собственные динамические свойства систем, настроенных по МО и СО, можно приближенно описать инерционным звеном первого порядка:
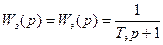
где Тэ =2То, для системы, настроенной на МО, и Тэ = 4То, для системы, настроенной на СО. В числителе передаточной функции (9.44) присутствует форсирующий сомножитель 4T01р+1, из-за которого в системе, настроенной на СО, переходный процесс по каналу хз … y обладает значительным перерегулированием (рисунок 9.17, б). В передаточную функцию (9.45) в качестве сомножителя входит реальное дифференцирующее звено с постоянной времени Т02, вследствие чего переходный процесс по каналу хз … y в системе, настроенной на МО, имеет большую длительность, чем в системе, настроенной на СО.
Осуществление инвариантности в стабилизирующих и следящих системах
Одной из главных целей синтеза автоматической системы является обеспечение требуемой точности в установившихся и переходных режимах. Точность систем в установившихся режимах можно улучшить, увеличивая порядок астатизма и коэффициент разомкнутого контура. Но при этом, как правило, уменьшается запас устойчивости, увеличивается колебательность и, как следствие, ухудшается точность системы в переходных режимах.
Эффективным средством устранения противоречия между условиями точности в установившихся и переходных режимах служит компенсация внешних воздействий путем осуществления инвариантности.
Термин «инвариантность» означает независимость одной физической величины от другой. В теории автоматического управления рассматривают независимость выходных величин (управляемой величины или сигнала ошибки) от входных воздействий. В системах стабилизации стремятся получить независимость управляемой величины от возмущающего воздействия, а в следящих системах – независимость сигнала ошибки от задающего воздействия.
Инвариантность в автоматических системах достигается при помощи управления по возмущению: управляющее воздействие формируется в зависимости от изменений возмущающего воздействия. Очевидно, что этот принцип управления применим, если возмущающее воздействие может быть измерено. В разомкнутых цепях при помощи воздействий, называемых компенсирующими связями, может быть полностью или частично устранено влияние внешних возмущений на управляемую величину в переходных и установившихся режимах. Компенсирующие связи не образуют замкнутых контуров и поэтому не ухудшают устойчивости систем.
Рассмотрим алгоритмическую схему комбинированной системы стабилизации с компенсирующей связью по возмущению (рисунок 9.18).
Компенсирующая связь действует на выходную величину со знаком, который всегда противоположен знаку непосредственного влияния возмущения на выход.
Передаточная функция системы по возмущению
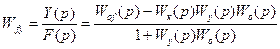, (9.47)
где Wo(p) и Wo¦(p) – передаточные функции объекта соответственно по управляющему и возмущающему воздействию; Wy(p) – передаточная функция управляющего устройства; Wк(p) – передаточная функция компенсирующего устройства.
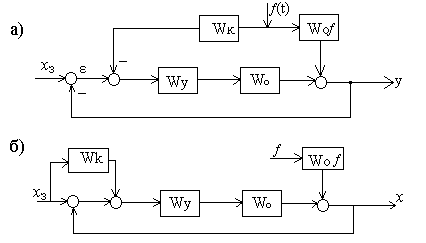
Рисунок 9.18 Алгоритмические структуры комбинированных систем управления с компенсирующими связями: а – по возмущению; б – по задающему воздействию.
Управляемая величина Y(t) не зависит от возмущения ¦(t), если передаточная функция равна нулю:
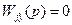(9.48)
а это возможно, если равен нулю ее числитель. Отсюдаусловие инвариантности стабилизируемой величиныпо отношению к возмущению:
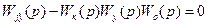(9.49)
Условие означает, что для достижения независимости величины Y(t) от возмущения ¦(t) необходимо, чтобы динамические свойства двух параллельных каналов, по которым возмущение ¦(t) действует на величину Y(t), были одинаковыми. Именно благодаря идентичности каналов, сигнал, поступающий на выход через звенья Wк(p), Wy(p) и Wo(p) компенсирует сигнал, идущий на выход через звено Wo¦(p).
Согласно условию инвариантности передаточная функция компенсирующего устройства:
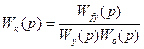(9.50)
Компенсирующее устройство представляет собой динамическое звено, свойства которого зависят от соотношения инерционностей канала возмущения Wo¦ и канала управления WyWo. Если инерционность канала управления больше, чем инерционность канала возмущения, то компенсирующее устройство должно обладать свойствами дифференцирующего звена. Причем, чем больше разница этих инерционностей, тем выше должен быть порядок дифференцирующего звена. Как известно, дифференцирующие звенья высокого порядка трудно технически реализовать.
Для обеспечения инвариантности только в статике компенсирующее устройство может быть реализовано в виде безинерционного звена с передаточным коэффициентом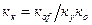 
В следящих системах необходимо добиваться независимости сигнала ошибки от задающего воздействия. Для схемы, приведенной на рисунке 9.18, б, передаточная функция между задающим воздействием хз(t) и сигналом ошибки ε (t):
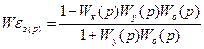, (9.51)
Приравнивая функцию (9.51) к нулю, находим условие инвариантности ошибки слежения по отношению к задающему воздействию:
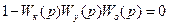, (9.52)
Отсюда требуемая передаточная функция компенсирующего устройства.
Компенсирующее устройство в следящих системах так же, как и в стабилизирующих, должно обладать дифференцирующими свойствами. По виду передаточных функций (9.51) и (9.52) можно установить, что введение компенсирующих связей не изменяет характеристический полином системы и, следовательно, не влияет на ее устойчивость. Очевидно также, что и в стабилизирующей, и в следящей системах инвариантность осуществима благодаря наличию двух параллельных каналов передачи сигналов от точки приложения воздействия до выходной величины (Y или ε). Этот структурный признак достижения инвариантности был впервые сформулирован акад. Б.Н. Петровым в виде принципа двухканальности. Но наличие двух каналов является лишь необходимым условием получения инвариантности. Достаточным условием служит условие физической реализуемости передаточной функции Wк(p), в виде конкретного технического устройства: максимальная степень полинома числителя должна быть меньше или равна максимальной степени полинома знаменателя.
Если передаточная функция Wк(p) удовлетворяет условию физической реализуемости, то в системе возможно достижение абсолютной инвариантности. Если же передаточная функция Wк(p) не удовлетворяет этому условию и может быть реализована только приближенно, то в системе осуществима лишь частичная инвариантность. В системе с частичной инвариантностью независимость достигается только при медленных изменениях входных воздействий.
Дата добавления: 2015-04-25; просмотров: 1722;