Синтез параллельной коррекции по обратным АФЧХ

Рисунок 9.10 Включение параллельного корректирующего устройства в САУ

Как правило, задача синтеза параллельного корректирующего устройства состоит в выборе схемы и определении параметров корректирующей обратной связи. Рассмотрим решение этой задачи с использованием обратных АФЧХ САУ.

Для САУ, показанной на рисунке 9.10, справедливо следующее равенство:

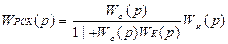(9.12)

Перейдя от передаточной функции к частотной передаточной функции, получим АФЧХ разомкнутой скорректированной системы W_р.ск.(j ).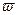

Обратная АФЧХ выражается следующим равенством:

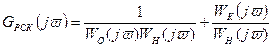(9.13)

I-я составляющая 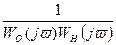- обратная АФЧХ разомкнутой нескорректированной системы.

II-я составляющая 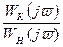– отношение АФЧХ коррекции к АФЧХ звена, охваченного обратной связью. С учетом вышесказанного, выражение (9.13) можно записать другим способом:

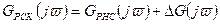, (9.14)

где ;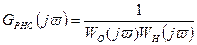

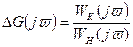
Применим к САУ критерий устойчивости Найквиста для обратной АФЧХ: замкнутая САР устойчива, если обратная АФЧХ разомкнутой системы охватывает критическую точку (-1,jv). Построим частотный годограф для G_р.нс.(jv) (рисунок 9.11).

Рисунок 9.11 Годограф Найквиста для обратной АФЧХ

Таким образом, при использовании метода обратной АФЧХ задача расчета корректирующей обратной связи сводится к отысканию 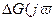), обеспечивающей необходимую деформацию обратной АФХ разомкнутой системы так, чтобы замкнутая система была бы устойчивой и удовлетворяла требованиям к запасам устойчивости и колебательности M системы.

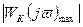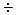Для удовлетворительного качества переходного процесса значение M должно быть в пределах M= =1,1 1,5

При этом геометрическим местом точек постоянной колебательности в плоскости G_нс.(jv) является окружность с центром в точке (-1, j0) и радиусом r=1/M (рисунок 9.11).

Чтобы САР была устойчивой и имела заданную колебательность (а, следовательно, и запасы устойчивости) G_р.ск.(jv) должна охватывать точку (-1, j0) и касаться окружности r=1/M.

Рассмотрим следующий пример. Пусть имеется следящая САУ с главной обратной связью по скорости (рисунок 9.12).

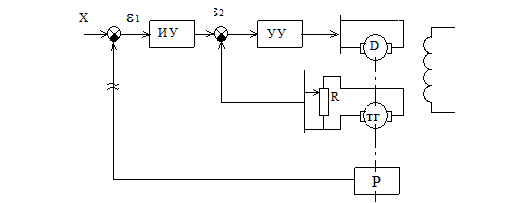
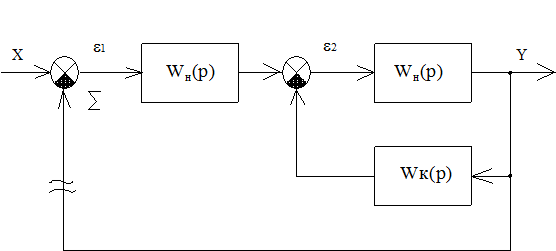
Рисунок 9.12 Функциональная (а) и структурная (б) схемы следящей САУ

В систему также введена корректирующая обратная связь по скорости, подаваемая с выхода тахогенератора ТГ через делитель R на вход усилительного устройства УУ (см. рисунок 9.12).

Комплексные коэффициенты усиления звеньев системы:

1) Wн(jv)=K_u, где K_u – коэффициент усиления безынерционной измерительной схемы с учетом передаточного числа редуктора.

2) Wк(jv)=K_ТГjv, где Kтг – крутизна характеристики ТГ с учетом делителя напряжения.

Передаточная функция звеньев, охваченных корректирующей обратной связью:

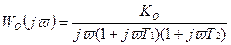(9.15)

Kо,T₁, T₂ – параметры охваченных звеньев.

Найдем выражение для корректирующего вектора обратной АФЧХ:

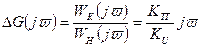(9.16)

При построении необходимо учесть, что (9.16) – чисто мнимая величина, и ее годограф совпадает с мнимой осью.

По абсолютному значению 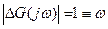. По этой причине 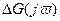будем откладывать вертикально для сответствующей v от Gнс.(jv). Алгоритм расчета корректирующего устройства выглядит следующим образом (см. рисунок 9.13):

Рисунок 9.13 Расчет звена параллельной коррекции методом обратных АФЧХ

1) Строим G_нс(jv);

2) Строим окружность M=const, r=1/M. Примем M=1,5;

3) Для различных частот определяем 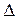G(jv)=l и откладываем их вертикально от кривой G_нс(jv) так, чтобы G_ск(jv) коснулась или была бы выше окружности M=const. Такой характеристике G_ск.(jv) соответствует определенное значение К_тг. Оно и будет искомым.