Синтез последовательных корректирующих устройств по логарифмическим характеристикам

Так как асимптотические ЛАХ достаточно просто строятся по виду 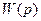, этот метод широко распространился в инженерной практике. Одновременно с построением ЛАХ проверяется и устойчивость и параметры качества и производится синтез корректирующих элементов.

При синтезе коррекции основной задачей является построение желаемой ЛАХ. Рекомендации по построению:

1) ЛАХ нескорректированной системы и желаемая ЛАХ (ЛАХ скорректированной системы) должны в возможно более широком диапазоне частот совпадать друг с другом. В противном случае, реализация корректирующих устройств усложняется. Для статической системы начальный участок горизонтален. Для астатической системы наклон начального участка должен быть -20n дб/дек (n – порядок астатизма системы). Низкочастотная асимптота при v =1 имеет ординаты 20 lg(k), где k – коэффициент усиления системы.

2) Если задана динамическая ошибка системы D₁ в режиме низкочастотных гармонических колебаний управляющего воздействия при частоте v₁, то есть контрольная точка выше которой должна проходить желаемая ЛАХ. D_дин =½W_p^-1(jv)½×А₁, где А₁ – амплитуда, х_вх – (управляющее воздействие), Х=А₁×sin(v_i×t). ½W_p(jv_i)½- модуль комплексного коэффициента усиления разомкнутой системы.

Тогда

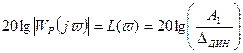(9.1)

Проведение желаемой ЛАХ на 3 дб выше точки с координатами L(v) и v₁ обеспечит динамическую ошибку не больше заданной.

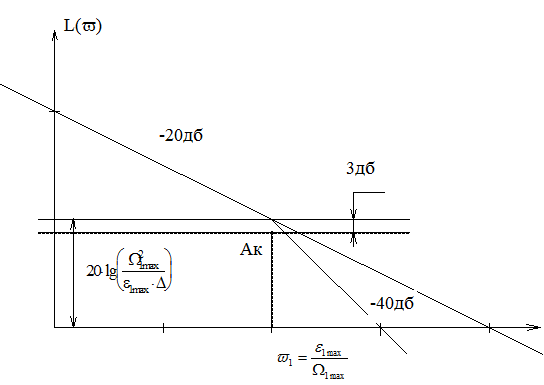
Рисунок 9.1 К построению желаемой ЛАХ

Динамическая ошибка равна частному от деления амплитуды управляющего воздействия на модуль комплексного коэффициента усиления.

3) Построение среднечастотной асимптоты начинают с выбора частоты среза v_с. При v_с , когда L_m=20lgA=20 lg½W_p(jv_i)½=0, наклон желаемой ЛАХ желательно выбирать – 20 дб/дек. При этом в минимально-фазовых системах будет обеспечена устойчивость и необходимый запас по фазе.

4) Требуемая частота среза может быть приблизительно оценена следующим образом. Если задана допустимая ошибка D_max и оговорены только максимальная скорость W_1max и максимальное ускорение e_1max входного воздействия, то может быть подобрано эквивалентное гармоническое входное воздействие, у которого амплитуды скорости и ускорения равны максимальным заданным значениям т.е.

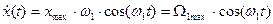; (9.2)

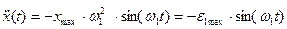. (9.3)

откуда 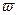₁= 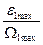; x_max= .

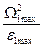тогда ордината контрольной точки

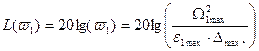(9.4)

Среднечастотный участок L_ж ограничен условиями требуемых запасов по фазе g и модулю h. Для этого используют специальную номограмму постоянных ВЧХ Рс плоскости g и h. Для этого строят ВЧХ и по заданному Р_max определяют Р_min=1-Р_max. На графике номограммы строят прямоугольник определяемый касательными к линиям Рmin и Рmax. По оси ординат определяют h, равный половине высоты прямоугольника, а по оси абсцисс – запас по фазе g, равный половине основания этого прямоугольника. Значения запаса устойчивости по модулю ± h ограничивает среднечастотный участок.

Для определения запасов устойчивости h и g можно воспользоваться кривыми (рисунок 9.2).

v_с= 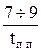или если даны t_пп и s

v_с= 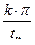где t_{пп –} заданное время переходного процесса.

k – коэффициент определяется в функции заданного перерегулирования.

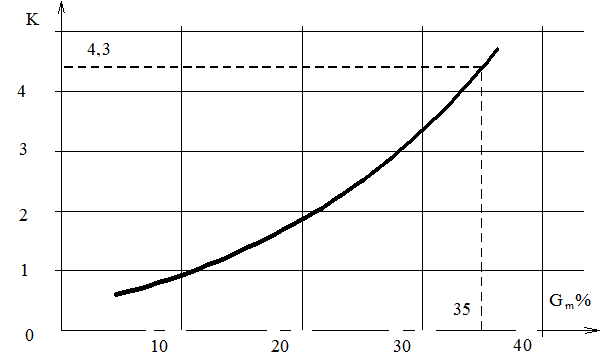
Рисунок 9.2 Номограмма для определения запасов устойчивости

5) Желательно, чтобы наклоны желаемой ЛАХ меньше отличались от наклонов ЛАХ нескорректированой системы.

6) Желаемую ЛАХ скорректированной системы можно строить по номограммам в соответствии с заданными s_m, t_п, t_m, M (их можно найти в специализированной литературе).

При использовании последовательной коррекции W_ск(p)=W_нс × W_к.пс(p)

Для логарифмов модулей:

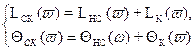(9.5)

Характеристики корректирующего устройства из (9.5):

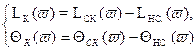(9.6)

Из (9.6) видно что ЛАХ корректирующего устройства найдется, если из ЛАХ желаемой скорректированной системы L_ск(v) вычесть ЛАХ нескорректированной системы L_нс(v).

Далее по найденной L_к(v) подбирается схема корректирующего устройства и рассчитываются численные параметры.

Рассмотрим это на примере.

Дано: ЛАХ L_нс(v) системы с W(p)= 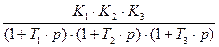, где T₁>T₂>T₃ т.е. три инерционных звена соединенных последовательно, а также задано время переходного процесса t_ПП

Рисунок 9.3. К примеру синтеза последовательного корректирующего устройства

Порядок синтеза

1) Строим L_нс(v) и Q_нс(v).

2) Строим желаемую ЛАХ L_ск(v) и Q_нс(v) так чтобы она больше совпадала с L_нс(v), чтобы при v_ср наклон был -1 и чтобы удовлетворялся g_с и v_с= .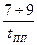

3) v¢ – обычно находится из построения, а v¢¢ из уравнения фаз при v¢_с. Запишем это уравнение.

В общем случае АФХ для разомкнутой цепи последовательно соединенных звеньев:

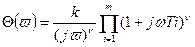, (9.7)

где

n – порядок астатизма системы;

n_i > 0 – форсирующие свенья;

n_i < 0 – инерционные звенья.

Точные уравнения ЛАХ и ФЧХ для уравнений (9.5 и 9.6):

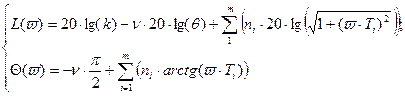(9.8)

Уравнение (9.8) записывают для скорректированой системы.

а) Левую часть Q(v_ср) записывают с учетом заданного запаса по фазе g_ср.

б) В правую часть записывают члены для v=v_ср и для T_i= 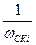, соответствующие изломам L_ск(v)

Поскольку L_ск(v) претерпевает один излом при неизвестной частоте v_сп^¢¢, то требуется ее определение из (9.8).

4) Вычитают L_ск(v)-L_нс(v)=L_к(v) и получают L_к(v).

Теперь задача подобрать схему корректирующего звена с такой характеристикой. В литературе обычно даются эти схемы (таблица 9.1)

Таблица 9.1