Число степеней свободы

Статистические оценки параметров теоретического распределения являются случайными величинами, так как получаются они на основе случайной выборки. Для многих задач математической статистики (построение доверительных интервалов, проверка статистических гипотез и т.д.) оказывается необходимым рассмотрение законов распределения статистических оценок или их комбинаций. При этом широко используются такие законы распределения случайных величин, как хи-квадрат ( 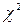), Фишера-Снедекора, Стьюдента и некоторые другие.

В выражениях указанных законов распределения входят величины, называемые степенями свободы.

Любая композиция k независимых случайных величин Х₁, Х₂, …Х_k, в частности сумма, имеет k степеней свободы, так как каждая составляющая может менять свое значение независимо от других значений. Различные независимые измерения одной и той же величины можно рассматривать как различные случайные величины с числом степеней свободы, равным числу измерений. Так, например, последовательность измерений Х₁, Х₂, …Х_k или их сумма имеет k степеней свободы. Точно так же и сумма квадратов этих величин имеет k степеней свободы.

Однако если для рассмотренной системы случайных величин задана некоторая связь, то количество степеней свободы уменьшается. В частности, если найти среднее значение полученных в результате выборки значений х₁, х₂, …х_{k :}

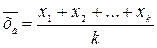
и зафиксировать это значение для соответствующих k случайных величин Х₁, Х₂, …Х_k, т.е. признать верным выражение

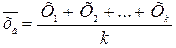
Для всех значений этих величин, то одну из величин всегда можно выразить через остальные. Это означает, что она оказалась связанной и система случайных величин потеряла одну степень свободы.

Если после фиксации выборочной средней и выборочной дисперсии 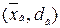рассматривать случайную величину, зависящую от k независимых случайных величин и от 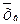, , 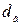то ее число степеней свободы будет меньше еще на единицу.

В некоторых случаях фиксируются не только общая выборочная средняя и общая выборочная дисперсия, но и групповые средние и групповые дисперсии. Тогда число степеней свободы у системы случайных величин сокращается на число таких связей.

Лекция 2

План

1. Точечная и интервальная оценки. Доверительный интервал.

2. Метод моментов для точечной оценки параметров распределения.

3. Метод наибольшего правдоподобия для точечной оценки параметров распределения.

4. Доверительный интервал для оценки математического ожидания нормального распределения.

5. Основные законы распределения статистических оценок.

6. Доверительный интервал для оценки среднего квадратичного отклонения нормального распределения