Основные законы распределения статистических законов

Распределение статистических оценок в большинстве случаев достаточно точно описывается такими законами распределения, как нормальный, хи-квадрат, Стьюдента, Фишера-Снедекора.

Нормальным называется такое распределение случайной величины Х, плотность вероятности которого описывается функцией

,

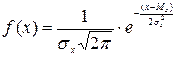где и М_х – среднее квадратичное отклонение и математическое ожидание случайной величины.

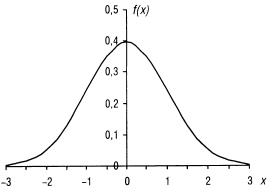
Нормальный закон распределения называют также законом Гаусса. График функции плотности вероятности нормального распределения имеет вид:

Распределением c2 (хи-квадрат) с k степенями свободы называется распределение квадратов k независимых случайных величин, распределенных по нормальному закону, т.е.

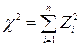
Плотность вероятности c2–распределения

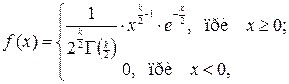
где 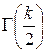– гамма-функция, для которой определяется равенство .

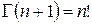Распределением Стьюдента или t–распределением называется распределение случайной величины

,

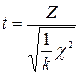где Z – случайная величина, распределенная по стандартному нормальному закону,

c2 – независимая от Z случайная величина, имеющая c2-распределение с k степенями свободы.

Плотность вероятности

,

где 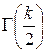– гамма-функция.

Распределением Фишера-Снедокора или F – распределением называется распределение случайной величины

,

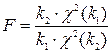где c2(k1) и c2(k2) – случайные величины, имеющие c2–распределение с k1 и k2 степенями свободы соответственно.

Плотность вероятности

,

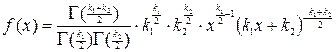где 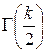– гамма-функция.