Доверительный интервал для оценки среднего квадратичного отклонения нормального распределения

Пусть известно, что случайная величина Х имеет нормальное распределение. Во-первых, требуется оценить неизвестное среднее квадратичное отклонение 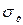по «исправленному» выборочному среднему квадратичному отклонению s. Во-вторых, необходимо найти доверительный интервал, в который попадает 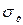с заданной надежностью .

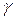Без вывода запишем доверительный интервал:

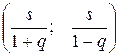
Задавая значения n и 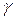можно определить q.

Пример. Пусть величина Х имеет нормальное распределение. Проведена выборка, объем которой n=25, и найдено «исправленное» выборочное среднее квадратичное отклонение 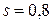. Найти доверительный интервал, покрывающий 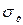с надежность .

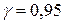Решение. По таблице зависимости n, q и 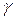находим значение q=0,32. После этого определяем доверительный интервал 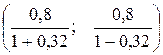, т.е. (0,16; 1,18).