Переменный ток

Установившиеся вынуж­денные электромагнитные колебания мож­но рассматривать как протекание в цепи, содержащей резистор, катушку индуктив­ности и конденсатор, переменного тока. Переменный токможно считать квазиста­ционарным,т. е. для него мгновенные зна­чения силы тока во всех сечениях цепи практически одинаковы, так как их изме­нения происходят достаточно медленно, а электромагнитные возмущения распро­страняются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа.

Рассмотрим последовательно процес­сы, происходящие в цепи, содержащей резистор, катушку индуктивности и кон-

содержащей резистор, катушку индуктивности и конденсатор, при приложении к ней перемен­ного напряжения

U=U_mcoswt, (15-33)

где U_m — амплитуда напряжения.

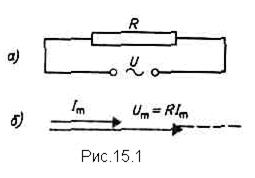
Переменный ток, текущий через ре­зистор сопротивлениемR (L®0, С®0) (рис.15.1, а). При выполнении условия квазистационарности ток через резистор определяется законом Ома:

I=U/R=(U_m/R)coswt=I_mcoswt,

где амплитуда силы тока l_m=U_m/R.

Для наглядного изображения соотно­шений между переменными токами и на­пряжениями воспользуемся методом век­торных диаграмм. На рис. 15.1, б дана век­торная диаграмма амплитудных значений тока I_m и напряжения U_m на резисторе (сдвиг фаз между I_m и U_m равен нулю).

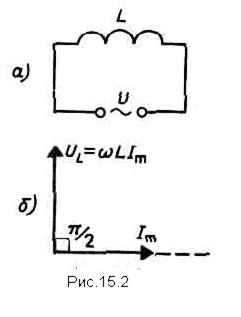
Переменный ток, текущий через ка­тушку индуктивностьюL (R®0, C®0) (рис. 15.2, а). Если в цепи приложено пере­менное напряжение (15-33), то в ней по­течет переменный ток, в результате чего возникнет э.д.с. самоиндукции

ξ_s=-LdI/dt. Тогда закон Ома для рассматриваемого участка цепи имеет вид

U_mcoswt-LdI/dt=0,

откуда

LdI/dt=U_mcosw . (15-34)

Так как внешнее напряжение приложено к катушке индуктивности, то

U_L=LdI/dt (15-35)

есть падение напряжения на катушке. Из уравнения (15-34) следует, что

dI=(U_m/L)coswt/dt,

или после интегрирования, учитывая, что постоянная интегрирования равна

нулю (так как отсутствует постоянная составля­ющая тока), получим

(15-36)

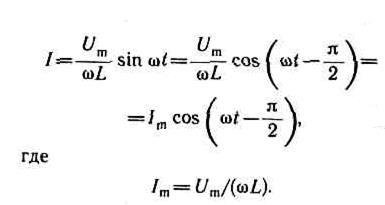
Величина

R_L=wL (15-37)

называется реактивным индуктивным со­противлением(или индуктивным сопро­тивлением).Из выражения (15-36) выте­кает, что для постоянного тока (w=0) катушка индуктивности не имеет сопротив­ления. Подстановка значения U_m=wLI_m в выражение (15-34) с учетом (15-35) приводит к следующему значению падения напряжения на катушке индуктивности:

U_L=wLI_mcoswt. (15-38)

Сравнение выражений (15-36) и (15-38) приводит к выводу, что падение напряже­ния U_L опережает по фазе ток I, текущий через катушку, на p/2, что и показано на векторной диаграмме (рис. 15.2, б).

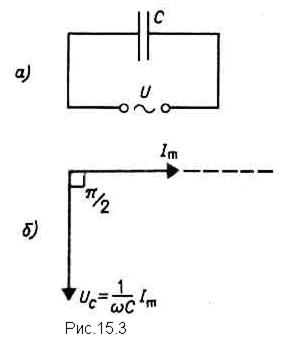
Переменный ток, текущий через конденсатор емкостьюС (R®0, L®0)

Если переменное напряже­ние приложено к конденсатору, то он все время перезаряжается, и в цепи потечет переменный ток. Так как все внеш­нее напряжение приложено к конденсато­ру, а сопротивлением подводящих прово­дов можно пренебречь, то

Q/C=U_C=U_mcoswt.

Сила тока (15-38)

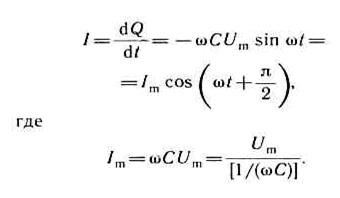
Величина

R_C=1/(wС)

называется реактивным емкостным сопро­тивлением(или емкостным сопротивлени­ем).Для постоянного тока (w=0) R_C=¥, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе

U_C=(1/wC)I_mcoswt. (15-39)

Сравнение выражений (15-38) и (15-39) приводит к выводу, что падение напряже­ния U_C отстает по фазе от текущего через конденсатор тока I на p/2. Это показано на векторной диаграмме (рис. 15.3, б).

Цепь переменного тока, содержа­щая последовательно включенные ре­зистор, катушку индуктивности и конден­сатор.На рис. 15.4,а представлена цепь, содержащая резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, на концы которой подается переменное напряжение. В цепи возникнет переменный ток, который вы­зовет на всех элементах цепи соответству­ющие падения напряжения U_R, U_L и U_C. На рис. 15.4, б представлена векторная ди­аграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и кон­денсаторе (U_C). Амплитуда U_m приложен­ного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как видно из рис. 15.4, б, угол j определяет разность фаз между напряжением и силой тока. Из рисунка следует, что

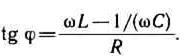(15-40)

Из прямоугольного треугольника получаем,

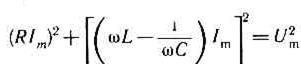
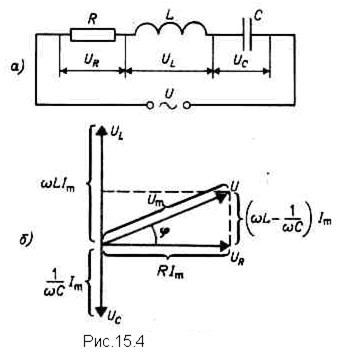
откуда амплитуда силы тока имеет значение

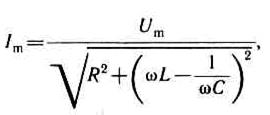(15-41)

Таким образом, если напряжение в це­пи изменяется по закону

U=U_mcoswt,

то в цепи течет ток

I = I_mcos(wt-j), (15-42)

где j и I_m определяются соответственно формулами (15-41) и (15-42). Величина

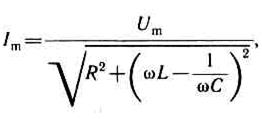(15-43)

называется полным сопротивлением цепи, а величина

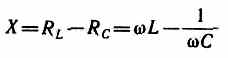
— реактивным сопротивлением.

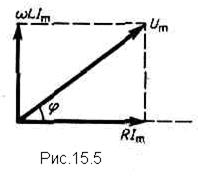
Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L в сумме равны приложенному напряже­нию U. Векторная диаграмма для данного случая представлена на рис. 15.5, из кото­рого следует, что

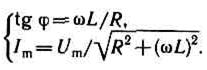(15-44)

Отсутствие конден­сатора в цепи означает С=¥, а не С=0.