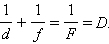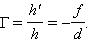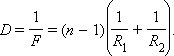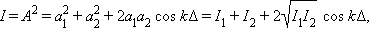Переменный ток 4 страница
Зеркальное и диффузное отражение.
В зависимости от свойств границы раздела между двумя средами отражение может иметь различный характер. Если граница имеет вид поверхности, размеры неровностей которой меньше длины световой волны, то она называется зеркальной.
Лучи света, падающие на такую поверхность узким параллельным пучком, идут после отражения также по близким направлениям. Такое направленное отражение называют зеркальным.
Если же размеры неровностей больше длины волны света, то узкий пучок рассеивается на границе. После отражения лучи света идут по всевозможным направлениям. Такое отражение называют рассеянным или диффузным. Именно благодаря диффузному отражению света мы можем видеть предметы, которые сами не излучают свет. В малой степени рассеяние света имеет место при его отражении даже от самой гладкой поверхности, например, от обычного зеркала. Иначе мы не могли бы увидеть поверхность зеркала.
Закон отражения света.
Закон отражения света определяет взаимное расположение падающего луча, отраженного луча и перпендикуляра к поверхности, восстановленного в точке падения.
Этот закон справедлив для волн любой природы и формулируется так: падающий луч, отраженный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости; угол отражения g равен углу падения a
Очевидно, что этот закон будет выполняться и в том случае, если свет будет распространяться в обратном направлении. Обратимость хода световых лучей является их важным свойством.
Изображение в плоском зеркале.
Пусть светящаяся точка находится перед плоской отражающей свет поверхностью, т.е. плоским зеркалом. Поставим вопрос: где мы увидим изображение этой точки, если посмотрим в зеркало? Для ответа на этот вопрос рассмотрим несколько лучей,выходящих из точки S и попадающих после отражения в глаз наблюдателя.
Человеку кажется, что лучи выходят из точки S1, которую можно найти, продолжив лучи в противоположную сторону до пересечения. Точка S1 поэтому будет являться изображением точки S в плоском зеркале. Это изображение называется мнимым, так как в точке S1 пересекаются не сами отраженные лучи, а их продолжения. Световая энергия в эту точку не поступает.
Рассмотрим любые два луча расходящегося пучка, например крайние лучи пучка, попадающего в глаз, - лучи AB и CD. В треугольниках SAC и S1AC сторона AC общая. Используя закон отражения, можно доказать, что углы в треугольниках, прилегающие к этой стороне, соответственно конгруэнтны. Следовательно, треугольники конгруэнтны и совместятся друг с другом, если перегнуть рисунок по линии зеркала. Это означает, что точка S1 расположена симметрично точке S относительно зеркала. Поэтому для нахождения изображения точки достаточно опустить из нее на зеркало или на его продолжение перпендикуляр и продолжить его на такое же расстояние за зеркало.
Закон преломления света.
На границе двух сред свет меняет направление своего распространения. Часть световой энергии возвращается в первую среду, т.е. происходит отражение света.
Если вторая среда прозрачна, то часть света при определенных условиях может пройти через границу сред, также меняя при этом, как правило, направление своего распространения. Это явление называется преломлением света.
Вследствие преломления наблюдается кажущееся изменение размеров, формы и расположения предметов. В этом нас могут убедить простые наблюдения. Установим наклонно карандаш в стакане с водой. Часть карандаша, находящаяся в воде, кажется сдвинутой в сторону и увеличенной в диаметре.
Подобные явления объясняются изменением напрвления лучей на границе двух сред. Луч, распространяющийся в первой среде и достигающий границы, называется падающим лучом. Он составляет с перпендикуляром к границе, проведенным через точку падения, угол a, называемый углом падения. Луч, прошедший во вторую среду, называют преломленным лучом. Угол b, который этот луч образует с тем же перпендикуляром, называют углом преломления.
Закон преломления, установленный экспериментально в XVII веке, формулируется следующим образом:
Падающий луч, преломленный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред.
Показатель преломления.
Постоянная величина, входящая в закон преломления света, называется относительным показателем преломления или показателем преломления одной среды относительно первой.
Показатель преломления среды относительно вакуума называют абсолютным показателем преломления этой среды. Он равен отношению синуса угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду. Относительный показатель преломления n связан с абсолютными показателями n2 и n1 первой среды соотношением:
Поэтому закон преломления может быть записан следующим образом:
Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой
Абсолютный показатель преломления среды имеет глубокий физический смысл. Он связан со скоростью распространения света в данной среде и зависит от физического состояния среды, в которой распространяется свет, т.е. от температуры, плотности вещества, наличия в нем упругих натяжений. Показатель преломления зависит также и от характеристик самого света. Для красного света он меньше, чем для зеленого, а для зеленого меньше, чем для фиолетового.
Полное внутреннее отражение.
Если n - показатель преломления стекла относительно воздуха (n>1), то показатель преломления воздуха относительно стекла будет равен 1/n. В данном случае стекло является первой средой, а воздух - второй. Закон преломления запишется так:
При этом угол преломления больше угла падения, т.к. sin b = n*sin a, а n>1; следовательно, sin b > sin a и следовательно, угол преломления больше угла падения (b > a). Значит, переходя в оптически менее плотную среду, луч отклоняется в сторону от перпендикуляра к границе двух сред. Наибольшему возможному углу преломления b = 90 соответствует угол падения a0.
При угле падения a > a0 преломленный пучок исчезнет, и весь свет отражается от границы раздела, т.е. происходит полное отражение света.
Тонкие линзы
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.
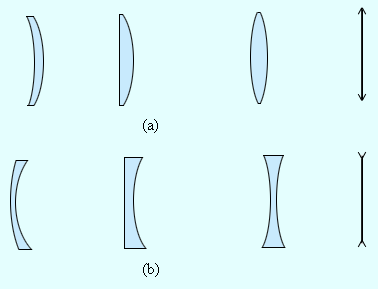
Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).
|
| Рисунок 3.3.1. Собирающие (a) и рассеивающие (b) линзы и их условные обозначения |
Прямая, проходящая через центры кривизны O1 и O2 сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O. Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называютсяпобочными оптическими осями.
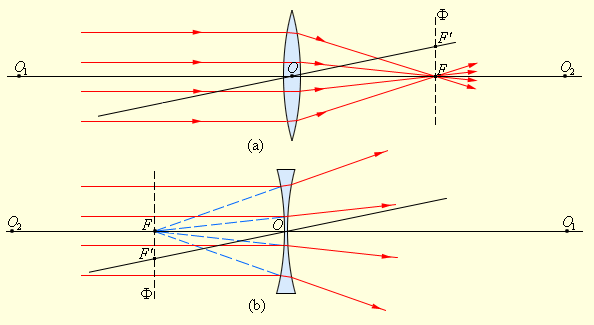
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку F', которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус (рис. 3.3.2). Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя той же буквой F.
|
| Рисунок 3.3.2. Преломление параллельного пучка лучей в собирающей (a) и рассеивающей (b) линзах. Точки O1и O2 – центры сферических поверхностей, O1O2 – главная оптическая ось, O – оптический центр,F – главный фокус, F' – побочный фокус, OF' – побочная оптическая ось, Ф – фокальная плоскость |
Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми и перевернутыми, действительными и мнимыми,увеличенными и уменьшенными.
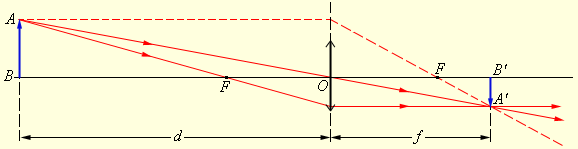
Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Примеры таких построений представлены на рис. 3.3.3 и 3.3.4.
|
| Рисунок 3.3.3. Построение изображения в собирающей линзе |
|
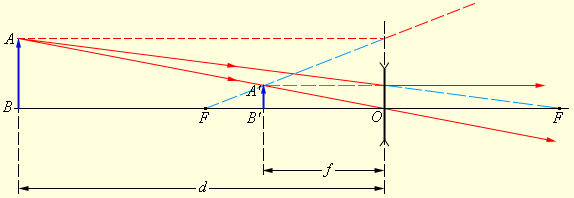
| Рисунок 3.3.4. Построение изображения в рассеивающей линзе |
Следует обратить внимание на то, что некоторые из стандартных лучей, использованных на рис. 3.3.3 и 3.3.4 для построения изображений, не проходят через линзу. Эти лучи реально не участвуют в образовании изображения, но они могут быть использованы для построений.
Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:
|
Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м:
| 1 дптр = м–1. |
Формула тонкой линзы аналогична формуле сферического зеркала. Ее можно получить для параксиальных лучей из подобия треугольников на рис. 3.3.3 или 3.3.4.
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.
Величины d и f также подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
d < 0 и f < 0 – для мнимых источников и изображений.
Для случая, изображенного на рис. 3.3.3, имеем: F > 0 (линза собирающая), d = 3F > 0 (действительный предмет).
По формуле тонкой линзы получим: 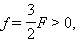 следовательно, изображение действительное.
следовательно, изображение действительное.
В случае, изображенном на рис. 3.3.4, F < 0 (линза рассеивающая), d = 2|F| > 0 (действительный предмет), 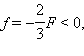 то есть изображение мнимое.
то есть изображение мнимое.
В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения h' и предмета h. Величине h', как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. Поэтому для прямых изображений Γ > 0, для перевернутых Γ < 0. Из подобия треугольников на рис. 3.3.3 и 3.3.4 легко получить формулу для линейного увеличения тонкой линзы:
|
В рассмотренном примере с собирающей линзой (рис. 3.3.3): d = 3F > 0, 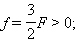 следовательно,
следовательно, 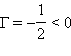 – изображение перевернутое и уменьшенное в 2 раза.
– изображение перевернутое и уменьшенное в 2 раза.
В примере с рассеивающей линзой (рис. 3.3.4): d = 2|F| > 0, 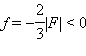 ; следовательно,
; следовательно, 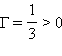 – изображение прямое и уменьшенное в 3 раза.
– изображение прямое и уменьшенное в 3 раза.
Оптическая сила D линзы зависит как от радиусов кривизны R1 и R2 ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула:
|
Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние d2 от первого изображения до второй линзы следует положить равным величине l – f1, где l – расстояние между линзами. Рассчитанная по формуле линзы величина f2определяет положение второго изображения и его характер (f2 > 0 – действительное изображение, f2 < 0 – мнимое). Общее линейное увеличение Γ системы из двух линз равно произведению линейных увеличений обеих линз: Γ = Γ1 · Γ2. Если предмет или его изображение находятся в бесконечности, то линейное увеличение утрачивает смысл.
Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея (см. § 3.5).
Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.
Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.
В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.
Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.
Фотоаппарат представляет собой замкнутую светонепроницаемую камеру. Изображение фотографируемых предметов создается на фотопленке системой линз, которая называется объективом. Специальный затвор позволяет открывать объектив на время экспозиции.
Особенностью работы фотоаппарата является то, что на плоской фотопленке должны получаться достаточно резкими изображения предметов, находящихся на разных расстояниях.
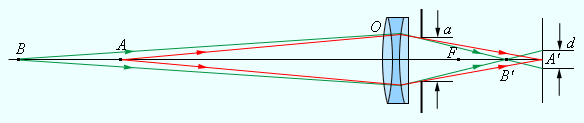
В плоскости фотопленки получаются резкими только изображения предметов, находящихся на определенном расстоянии. Наведение на резкость достигается перемещением объектива относительно пленки. Изображения точек, не лежащих в плоскости резкого наведения, получаются размытыми в виде кружков рассеяния. Размер d этих кружков может быть уменьшен путем диафрагмирования объектива, т.е. уменьшения относительного отверстия a / F (рис. 3.3.5). Это приводит к увеличению глубины резкости.
|
| Рисунок 3.3.5. Фотоаппарат |
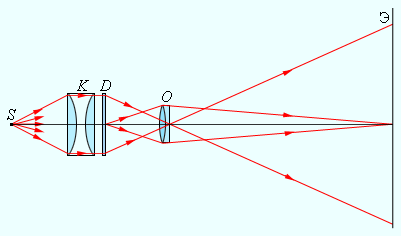
Проекционный аппарат предназначен для получения крупномасштабных изображений. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D) на удаленном экране Э (рис. 3.3.6). Система линз K, называемая конденсором, предназначена для того, чтобы сконцентрировать свет источника Sна диапозитиве. На экране Э создается действительное увеличенное перевернутое изображение. Увеличение проекционного аппарата можно менять, приближая или удаляя экран Э с одновременным изменением расстояния между диапозитивом D и объективом O.
|
5.2 Интерференция света
Интерференция световых волн
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.
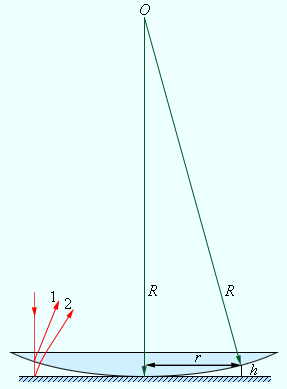
Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3.7.2).
|
| Рисунок 3.7.1. Наблюдение колец Ньютона. Интерференция возникает при сложении волн, отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн; h – толщина воздушного зазора |

|
| Рисунок 3.7.2. Кольца Ньютона в зеленом и красном свете |
Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов (см. § 3.6).
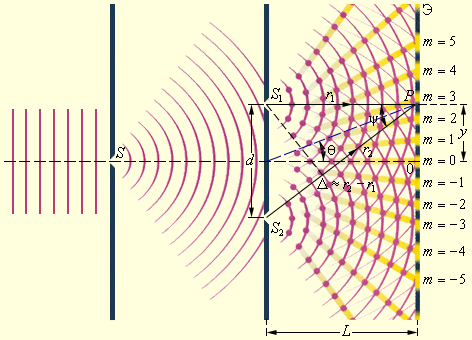
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
|
| Рисунок 3.7.3. Схема интерференционного опыта Юнга |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.
Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора 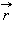 , записывается в виде
, записывается в виде
| E = a cos (ωt – kr), |
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
| E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ). |
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
| (*) |
где Δ = r2 – r1 – так называемая разность хода.
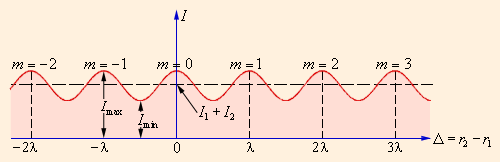
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, ...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивностиImin = (a1 – a2)2 < I1 + I2. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
|
| Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума |
В частности, если I1 = I2 = I0, т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
| (**) |
В этом случае Imax = 4I0, Imin = 0.
Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.
Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:
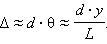
|
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
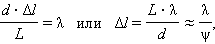
|
где ψ – угол схождения «лучей» в точке наблюдения P. Выполним количественную оценку. Допустим, что расстояние d между щелями S1 и S2 равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 105 нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика.
Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек.
В эксперименте Ньютона (рис. 3.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине 2hвоздушного промежутка между линзой и плоскостью. Для случая, когда радиус кривизны R линзы велик по сравнению с h, можно приближенно получить:
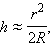
|
где r – смещение от оси симметрии. При написании выражения для разности хода следует также учесть, что волны 1 и 2 отражаются при разных условиях. Первая волна отражается от границы стекло–воздух, а вторая – от границы воздух–стекло. Во втором случае происходит изменение фазы колебаний отраженной волны наπ, что эквивалентно увеличению разности хода на λ / 2. Поэтому
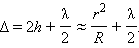
|
При r = 0, то есть в центре (точка соприкосновения) Δ = λ / 2; поэтому в центре колец Ньютона всегда наблюдается интерференционный минимум – темное пятно. Радиусы rm последующих темных колец определяются выражением
|
Эта формула позволяет экспериментально определить длину волны света λ, если известен радиус кривизны R линзы.
Проблема когерентности волн. Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волнодной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), в каких – интенсивности волн, т. е. квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос.
Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический (или случайный) характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10–8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τвся совокупность излучающих атомов обновляется. Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ. Отдельные «обрывки» излучения длительности τ называются цугами. Цуги имеют пространственную длину, равную cτ, где c – скорость света. Колебания в разных цугах не согласованы между собой. Таким образом, реальная световая волна представляет собой последовательность волновых цугов с беспорядочно меняющейся фазой. Принято говорить, что колебания в разных цугах некогерентны. Интервал времени τ, в течение которого фаза колебаний остается приблизительно постоянной, называют временем когерентности.
Дата добавления: 2015-06-01; просмотров: 1213;