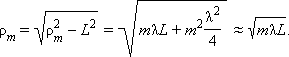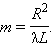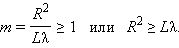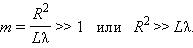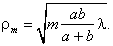Переменный ток 5 страница
Интерференция может возникнуть только при сложении когерентных колебаний, т. е. колебаний, относящихся к одному и тому же цугу. Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз оказывается случайной функцией времени. Интерференционные полосы испытывают беспорядочные перемещения из стороны в сторону, и за время Δt их регистрации, которая в оптических экспериментах значительно больше времени когерентности (Δt >> τ), происходит полное усреднение. Регистрирующее устройство (глаз, фотопластинка, фотоэлемент) зафиксирует в точке наблюдения усредненное значение интенсивности, равное сумме интенсивностей I1 + I2 обоих колебаний. В этом случае выполняется закон сложения интенсивностей.
Таким образом, интерференция может возникнуть только при сложении когерентных колебаний. Волны, создающие в точке наблюдения когерентные колебания, также называются когерентными. Волны от двух независимых источников некогерентны и не могут дать интерференции. Т. Юнг интуитивно угадал, что для получения интерференции света нужно волну от источника разделить на две когерентные волны и затем наблюдать на экране результат их сложения. Так делается во всех интерференционных схемах. Однако, даже в этом случае интерференционная картина исчезает, если разность хода Δ превысит длину когерентности cτ.

|
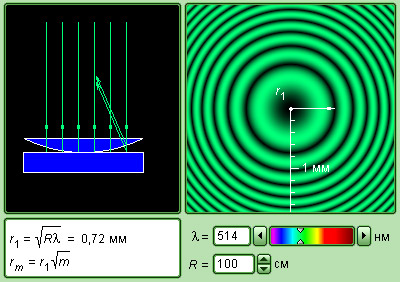
| Модель. Кольца Ньютона |
5.3 Дифракция света
Дифракция света
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него в 1818 г. французский ученый О. Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.
|
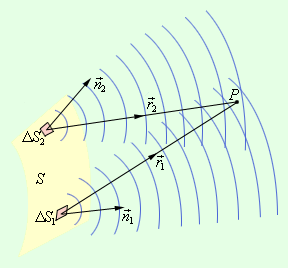
Рисунок 3.8.1.
Принцип Гюйгенса–Френеля. ΔS1 и ΔS2 – элементы волнового фронта, 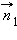 и и 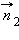 – нормали – нормали
|
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.
Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.
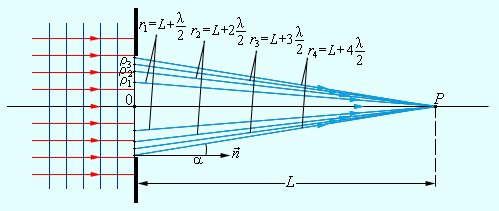
Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).
|
| Рисунок 3.8.2. Дифракция плоской волны на экране с круглым отверстием |
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A0 падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки Pдолжны отличается на половину длины волны, т. е.
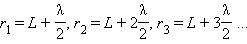
|
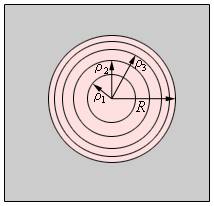
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).
|
| Рисунок 3.8.3. Границы зон Френеля в плоскости отверстия |
Из рис. 3.8.2 легко найти радиусы ρm зон Френеля:
|
Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R:
|
Здесь m – не обязательно целое число. Результат интерференции вторичных волн в точке P зависит от числа m открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:
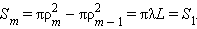
|
Одинаковые по площади зоны должны были бы возбуждать в точке наблюдения колебания с одинаковой амплитудой. Однако у каждой последующей зоны угол αмежду лучом, проведенным в точку наблюдения, и нормалью к волновой поверхности возрастает. Френель высказал предположение (подтвержденное экспериментом), что с увеличением угла α амплитуда колебаний уменьшается, хотя и незначительно:
| A1 > A2 > A3 > ... > A1, |
где Am – амплитуда колебаний, вызванных m-й зоной.
С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.
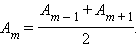
|
Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть
| A = A1 – A2 + A3 – A4 + ... = A1 – (A2 – A3) – (A4 – A5) – ... < A1. |
Таким образом, суммарная амплитуда колебаний в точке P всегда меньше амплитуды колебаний, которые вызвала бы одна первая зона Френеля. В частности, если бы были открыты все зоны Френеля, то до точки наблюдения дошла бы невозмущенная препятствием волна с амплитудой A0. В этом случае можно записать:
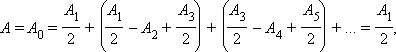
|
так как выражения, стоящие в скобках, равны нулю. Следовательно, действие (амплитуда), вызванное всем волновым фронтом, равно половине действия одной первой зоны.
Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность – в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастет. Например, если открыты 1, 3 и 5 зоны, то
| A = 6A0, I = 36I0. |
Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластинками.
При дифракции света на круглом диске закрытыми оказываются зоны Френеля первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна
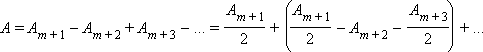
|
или A = Am + 1 / 2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то Am + 1 ≈ 2A0 и A ≈ A0, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.
Оценим размеры зон Френеля. Пусть, например, дифракционная картина наблюдается на экране, расположенном на расстоянии L = 1 м от препятствия. Длина волны света λ = 600 нм (красный свет). Тогда радиус первой зоны Френеля есть
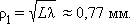
|
Таким образом, в оптическом диапазоне вследствие малости длины волны размер зон Френеля оказывается достаточно малым. Дифракционные явления проявляются наиболее отчетливо, когда на препятствии укладывается лишь небольшое число зон:
|
Это соотношение можно рассматривать как критерий наблюдения дифракции. Если число зон Френеля, укладывающихся на препятствии, становится очень большим, дифракционные явления практически незаметны:
|
Это сильное неравенство определяет границу применимости геометрической оптики. Узкий пучок света, который в геометрической оптике называется лучом, может быть сформирован только при выполнении этого условия. Таким образом, геометрическая оптика является предельным случаем волновой оптики.
Выше был рассмотрен случай дифракции света от удаленного источника на препятствиях круглой формы. Если точечный источник света находится на конечном расстоянии, то на препятствие падает сферически расходящаяся волна. В этом случае геометрия задачи несколько усложняется, так как теперь зоны Френеля нужно строить не на плоской, а на сферической поверхности (рис. 3.8.4).
|
| Рисунок 3.8.4. Зоны Френеля на сферическом фронте волны |
Расчет приводит к следующему выражению для радиусов ρm зон Френеля на сферическом фронте волны:
|
Все выводы изложенной выше теории Френеля остаются справедливыми и в этом случае.
Следует отметить, что теория дифракции (и интерференции) световых волн применима к волнам любой физической природы. В этом проявляется общность волновых закономерностей. Физическая природа света в начале XIX века, когда Т. Юнг, О. Френель и другие ученые развивали волновые представления, еще не была известна.

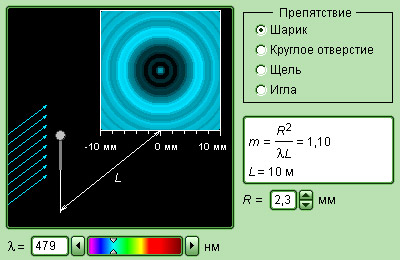
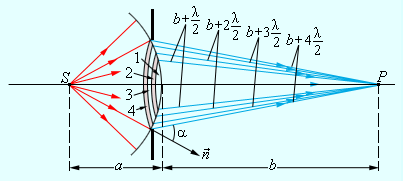
|
| Модель. Дифракция света |
5.4 Поляризация цвета
Поляризация света
В начале XIX века, когда Т. Юнг и О. Френель развивали волновую теорию света, природа световых волн была неизвестна. На первом этапе предполагалось, что свет представляет собой продольные волны, распространяющиеся в некоторой гипотетической среде – эфире. При изучении явлений интерференции и дифракции вопрос о том, являются ли световые волны продольными или поперечными, имел второстепенное значение. В то время казалось невероятным, что свет – это поперечные волны, так как по аналогии с механическими волнами пришлось бы предполагать, что эфир – это твердое тело (поперечные механические волны не могут распространяться в газообразной или жидкой среде).
Однако, постепенно накапливались экспериментальные факты, свидетельствующие в пользу поперечности световых волн. Еще в конце XVII века было обнаружено, что кристалл исландского шпата (CaCO3) раздваивает проходящие через него лучи. Это явление получило название двойного лучепреломления(рис. 3.11.1).
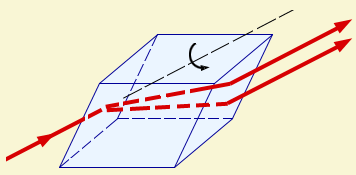
|
| Рисунок 3.11.1. Прохождение света через кристалл исландского шпата (двойное лучепреломление). Если кристалл поворачивать относительно направления первоначального луча, то поворачиваются оба луча, прошедшие через кристалл |
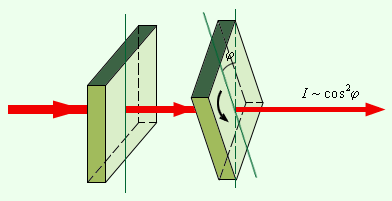
В 1809 году французский инженер Э. Малюс открыл закон, названный его именем. В опытах Малюса свет последовательно пропускался через две одинаковые пластинки из турмалина (прозрачное кристаллическое вещество зеленоватой окраски). Пластинки можно было поворачивать друг относительно друга на угол φ(рис. 3.11.2).
|
| Рисунок 3.11.2. Иллюстрация к закону Малюса |
Интенсивность прошедшего света оказалась прямо пропорциональной cos2 φ:
|
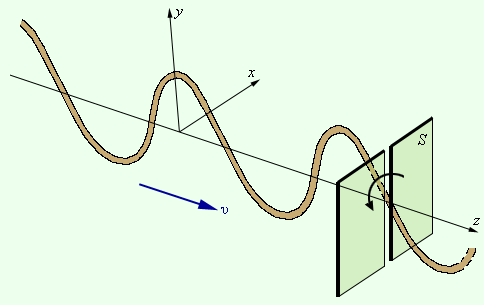
Ни двойное лучепреломление, ни закон Малюса не могут найти объяснение в рамках теории продольных волн. Для продольных волн направление распространения луча является осью симметрии. В продольной волне все направления в плоскости, перпендикулярной лучу, равноправны. В поперечной волне (например, в волне, бегущей по резиновому жгуту) направление колебаний и перпендикулярное ему направление не равноправны (рис. 3.11.3).
|
| Рисунок 3.11.3. Поперечная волна в резиновом жгуте. Частицы колеблются вдоль оси y. Поворот щели S вызовет затухание волны |
Таким образом, асимметрия относительно направления распространения (луча) является решающим признаком, который отличает поперечную волну от продольной. Впервые догадку о поперечности световых волн высказал в 1816 г. Т. Юнг. Френель, независимо от Юнга, также выдвинул концепцию поперечности световых волн, обосновал ее многочисленными экспериментами и создал теорию двойного лучепреломления света в кристаллах.
В середине 60-х годов XIX века на основании совпадения известного значения скорости света со скоростью распространения электромагнитных волн Ошибка! Недопустимый объект гиперссылки.сделал вывод о том, что свет – это электромагнитные волны. К тому времени поперечность световых волн уже была доказано экспериментально. Поэтому Максвелл справедливо полагал, что поперечность электромагнитных волн является еще одним важнейшим доказательством электромагнитной природы света.
Электромагнитная теория света приобрела должную стройность, поскольку исчезла необходимость введения особой среды распространения волн – эфира, который приходилось рассматривать как твердое тело.
В электромагнитной волне вектора 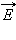 и
и 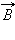 перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 2.6.3). Во всех процессах взаимодействия света с веществом основную роль играет электрический вектор
перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 2.6.3). Во всех процессах взаимодействия света с веществом основную роль играет электрический вектор 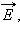 поэтому его называют световым вектором. Если при распространении электромагнитной волны световой вектор сохраняет свою ориентацию, такую волну называют линейно поляризованной или плоско поляризованной (термин поляризация волн был введен Малюсом применительно к поперечным механическим волнам). Плоскость, в которой колеблется световой вектор
поэтому его называют световым вектором. Если при распространении электромагнитной волны световой вектор сохраняет свою ориентацию, такую волну называют линейно поляризованной или плоско поляризованной (термин поляризация волн был введен Малюсом применительно к поперечным механическим волнам). Плоскость, в которой колеблется световой вектор 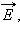 называется плоскостью колебаний (плоскость yz на рис. 2.6.3), а плоскость, в которой совершает колебание магнитный вектор
называется плоскостью колебаний (плоскость yz на рис. 2.6.3), а плоскость, в которой совершает колебание магнитный вектор 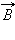 –плоскостью поляризации (плоскость xz на рис. 2.6.3).
–плоскостью поляризации (плоскость xz на рис. 2.6.3).
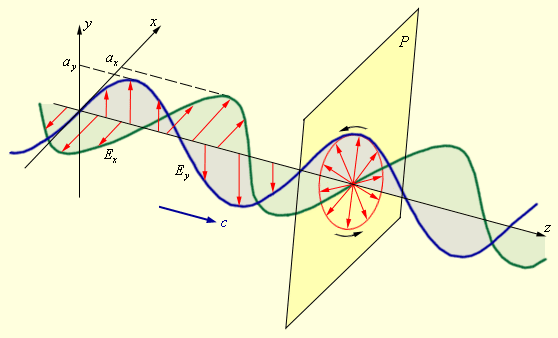
Если вдоль одного и того же направления распространяются две монохроматические волны, поляризованные в двух взаимно перпендикулярных плоскостях, то в результате их сложения в общем случае возникает эллиптически поляризованная волна (рис. 3.11.4).
|
| Рисунок 3.11.4. Сложение двух взаимно перпендикулярно поляризованных волн и образование эллиптически поляризованной волны |
В эллиптически поляризованной волне в любой плоскости P, перпендикулярной направлению распространения волны, конец результирующего вектора 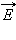 за один период светового колебания обегает эллипс, который называется эллипсом поляризации. Форма и размер эллипса поляризации определяются амплитудами ax иay линейно поляризованных волн и фазовым сдвигом Δφ между ними. Частным случаем эллиптически поляризованной волны является волна с круговой поляризацией (ax = ay, Δφ = ± π / 2).
за один период светового колебания обегает эллипс, который называется эллипсом поляризации. Форма и размер эллипса поляризации определяются амплитудами ax иay линейно поляризованных волн и фазовым сдвигом Δφ между ними. Частным случаем эллиптически поляризованной волны является волна с круговой поляризацией (ax = ay, Δφ = ± π / 2).
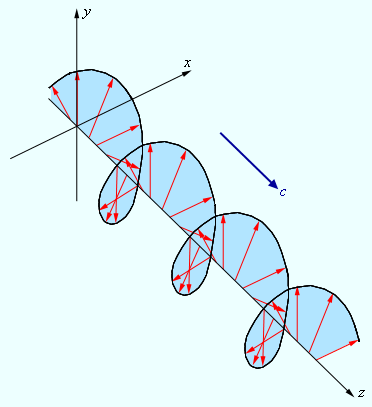
Рис. 3.11.5 дает представление о пространственной структуре эллиптически поляризованной волны.
|
| Рисунок 3.11.5. Электрическое поле в эллиптически поляризованной волне |
Линейно поляризованный свет испускается лазерными источниками. Свет может оказаться поляризованным при отражении или рассеянии. В частности, голубой свет от неба частично или полностью поляризован. Однако, свет, испускаемый обычными источниками (например, солнечный свет, излучение ламп накаливания и т. п.), неполяризован. Свет таких источников в каждый момент состоит из вкладов огромного числа независимо излучающих атомов (см. § 3.2) с различной ориентацией светового вектора в излучаемых этими атомами волнах. Поэтому в результирующей волне вектор 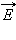 беспорядочно изменяет свою ориентацию во времени, так что в среднем все направления колебаний оказываются равноправными. Неполяризованный свет называют также естественным светом.
беспорядочно изменяет свою ориентацию во времени, так что в среднем все направления колебаний оказываются равноправными. Неполяризованный свет называют также естественным светом.
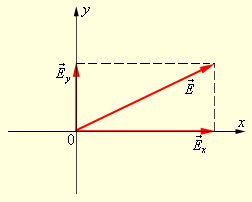
В каждый момент времени вектор 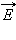 может быть спроектирован на две взаимно перпендикулярные оси (рис. 3.11.6).
может быть спроектирован на две взаимно перпендикулярные оси (рис. 3.11.6).
|
Рисунок 3.11.6.
Разложение вектора 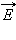 по осям по осям
|
Это означает, что любую волну (поляризованную и неполяризованную) можно представить как суперпозицию двух линейно поляризованных во взаимно перпендикулярных направлениях волн: 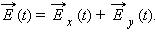 Но в поляризованной волне обе составляющие Ex (t) и Ey (t) когерентны, а в неполяризованной –Ошибка! Недопустимый объект гиперссылки., т. е. в первом случае разность фаз между Ex (t) и Ey (t) постоянна, а во втором она является случайной функцией времени.
Но в поляризованной волне обе составляющие Ex (t) и Ey (t) когерентны, а в неполяризованной –Ошибка! Недопустимый объект гиперссылки., т. е. в первом случае разность фаз между Ex (t) и Ey (t) постоянна, а во втором она является случайной функцией времени.
Явление двойного лучепреломления света объясняется тем, что во многих кристаллических веществах показатели преломления волн, линейно поляризованных во взаимно перпендикулярных направлениях, различны. Поэтому кристалл раздваивает проходящие через него лучи (рис. 3.11.1). Два луча на выходе кристалла линейно поляризованы во взаимно перпендикулярных направлениях. Кристаллы, в которых происходит двойное лучепреломление, называются анизотропными.
С помощью разложения вектора 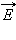 на составляющие по осям можно объяснить закон Малюса (рис. 3.11.2).
на составляющие по осям можно объяснить закон Малюса (рис. 3.11.2).
У многих кристаллов поглощение света сильно зависит от направления электрического вектора в световой волне. Это явление называют дихроизмом. Этим свойством, в частности, обладают пластины турмалина, использованные в опытах Малюса. При определенной толщине пластинка турмалина почти полностью поглощает одну из взаимно перпендикулярно поляризованных волн (например, Ex) и частично пропускает вторую волну (Ey). Направление колебаний электрического вектора в прошедшей волне называется разрешенным направлением пластинки. Пластинка турмалина может быть использована как для получения поляризованного света (поляризатор), так и для анализа характера поляризации света (анализатор). В настоящее время широко применяются искусственные дихроичные пленки, которые называются поляроидами. Поляроиды почти полностью пропускают волну разрешенной поляризации и не пропускают волну, поляризованную в перпендикулярном направлении. Таким образом, поляроиды можно считать идеальными поляризационными фильтрами.
Рассмотрим прохождение естественного света последовательно через два идеальных поляроида П1 и П2 (рис. 3.11.7), разрешенные направления которых повернуты друг относительно друга на некоторый угол φ. Первый поляроид играет роль поляризатора. Он превращает естественный свет в линейно поляризованный. Второй поляроид служит для анализа падающего на него света.

|
| Рисунок 3.11.7. Прохождение естественного света через два идеальных поляроида. yy' – разрешенные направления поляроидов |
Если обозначить амплитуду линейно поляризованной волны после прохождения света через первый поляроид через 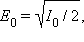 то волна, пропущенная вторым поляроидом, будет иметь амплитуду E = E0 cos φ. Следовательно, интенсивность I линейно поляризованной волны на выходе второго поляроида будет равна
то волна, пропущенная вторым поляроидом, будет иметь амплитуду E = E0 cos φ. Следовательно, интенсивность I линейно поляризованной волны на выходе второго поляроида будет равна
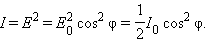
|
Таким образом, в электромагнитной теории света закон Малюса находит естественное объяснение на основе разложения вектора 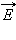 на составляющие.
на составляющие.
|
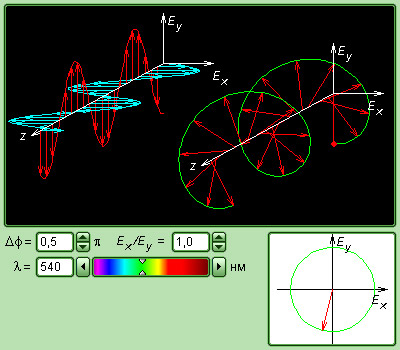
| Модель. Поляризация света |
Дата добавления: 2015-06-01; просмотров: 845;