Численное дифференцирование на основе интерполяционной формулы Лагранжа
Следуя (6.5), будем дифференцировать многочлен Лагранжа (6.15) по х как функцию от t:
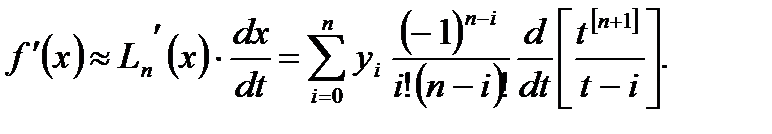
Учитывая, что согласно (6.9) 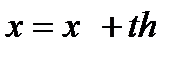 а также
а также 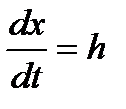 , получим окончательно:
, получим окончательно:
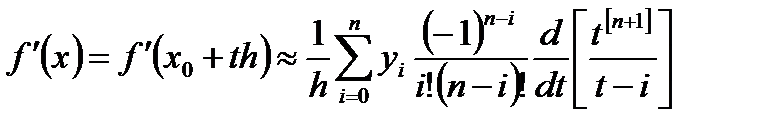 (6.16)
(6.16)
Пользуясь формулой (6.16), можно вычислять приближенные значения производной функции f(x), если она задана на отрезке [a;b] значениями в равноотстоящих узлах 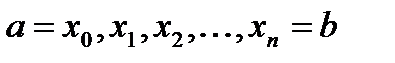 . Аналогично могут быть найдены производные функции f(x) высших порядков.
. Аналогично могут быть найдены производные функции f(x) высших порядков.
Пример 2.
Вычислить приближенное значение производной функции, заданной
таблицей 6.2 в точке х=4.
Таблица 6.2
| x | |||
| f(x) | ‑1 |
Используя формулу (6.16), получим (n=2, h=1):
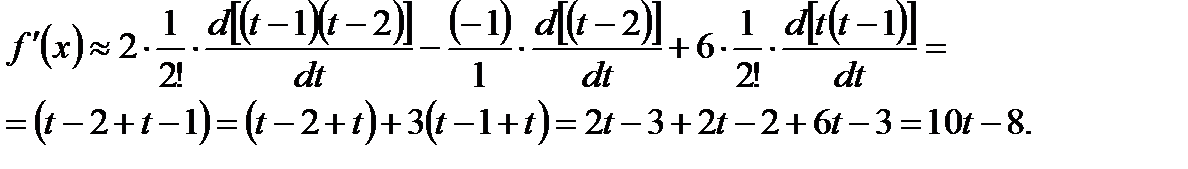
Учитывая, что узел х=4 соответствует значению t=1, т.е. 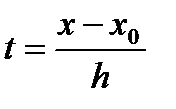 , получаем,
, получаем, 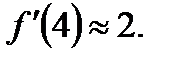
Если известно аналитическое выражение функции f(x), то формулудля оценки погрешности численного дифференцирования можно при этом же условии получить на основе формулы погрешности интерполирования:
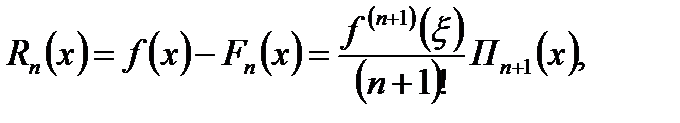 (6.17),
(6.17),
где 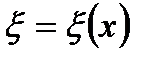 ‑ значение из отрезка [a;b], отличное от узлов и х.
‑ значение из отрезка [a;b], отличное от узлов и х.
Учитывая (6.7) и допуская, что f(x) дифференцируема п+1 раз, запишем:
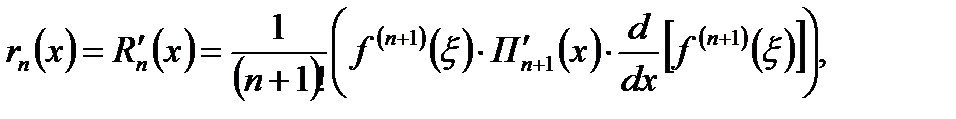 (16.18)
(16.18)
Формула (6.18) значительно упрощается, если оценка находится для значения производной 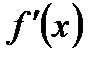 в узле xi таблицы. В этом случае, учитывая (6.14), получаем:
в узле xi таблицы. В этом случае, учитывая (6.14), получаем:
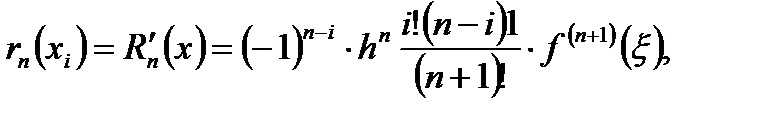 (6.19)
(6.19)
где  ‑ промежуточное значение между
‑ промежуточное значение между  . Обозначив
. Обозначив
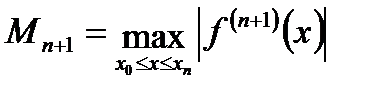 ,
,
получим верхнюю оценку абсолютной ошибки численного дифференцирования в узлах:
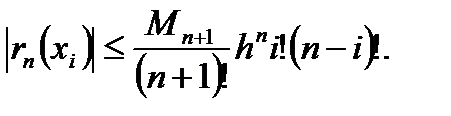 (6.20)
(6.20)
Дата добавления: 2015-04-03; просмотров: 4467;
