Интерполяционная формула Лагранжа для равноотстоящих узлов
Применяя для численного дифференцирования на отрезке [a;b] интерполяционный полином, естественно строить на этом отрезке систему равноотстоящих узлов
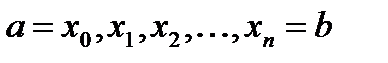 ,
,
Которыми отрезок делится на п равных частей:
 , (6.8)
, (6.8)
(i=0, 1, 2, п‑1).
В этом случае шаг интерполирования равен 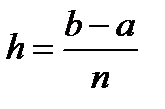 , а интерполяционный многочлен Лагранжа строится на равноотстоящих узлах и имеет более удобный вид. Положим
, а интерполяционный многочлен Лагранжа строится на равноотстоящих узлах и имеет более удобный вид. Положим
 . (6.9)
. (6.9)
С учетом формулы Лагранжа
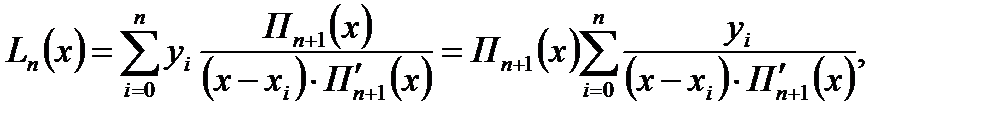 (6.10)
(6.10)
получим новые выражения для  . Учитывая, что
. Учитывая, что

и используя (6.9), последовательно находим:

т.е. в общем случае:
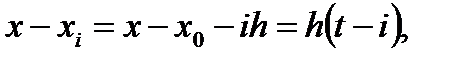 (6.11)
(6.11)
i=0, 1, …, п.
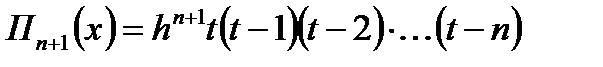 .
.
Обозначим

тогда выражение 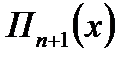 примет вид:
примет вид:
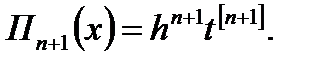 (6.12)
(6.12)
Учитывая, что при постоянном шаге имеет место
 i=0, 1, …, п,
i=0, 1, …, п,
последовательно находим:
 (6.13)
(6.13)
Заметим, что в (6.13) ровно п строк (i-тая отсутствует), причем значения разностей из первых i строк положительны, а остальных – отрицательны. Используя (6.13), получаем:
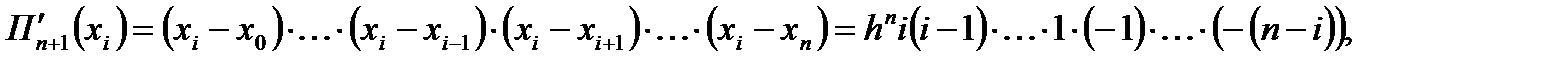 т.е.
т.е.
 (6.14)
(6.14)
С учетом представлений (6.12) и (6.14) формула Лагранжа (6.10) для равноотстоящих узлов принимает вид:
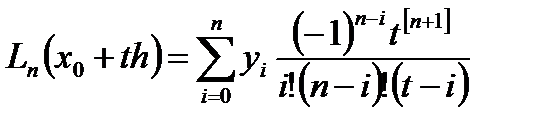 . (6.15)
. (6.15)
Пример 6.1.
Составить интерполяционный многочлен Лагранжа для функции, заданной своими значениями на равноотстоящих узлах (п=2, h=1):
Таблица 6.1
| x | |||
| f(x) | ‑2 |
Используя формулу (6.15), запишем:
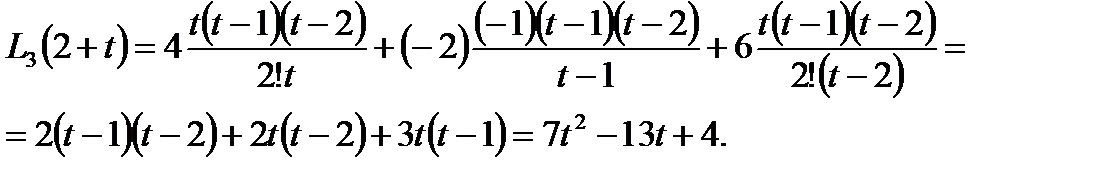
Дата добавления: 2015-04-03; просмотров: 4027;
