Комбинированный метод
Пусть f(a)f(b)<0и f'(x) и f''(x) сохраняют постоянные знаки на [a,b]. Соединяя метод хорд и касательных, получаем метод, на каждом этапе которого находится значение по недостатку и по избытку точного корня уравнения f(x)=0.
Процесс вычисления прекращаем, когда длина отрезка, на котором находится корень уравнения, будет меньше заданной точности ε. За значение корня лучше принять среднее арифметическое полученных последних значений.
Геометрическая интерпретация комбинированного метода:
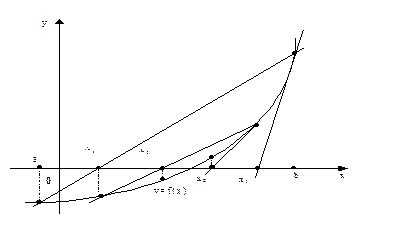Пример: Вычислить с точностью ε=0.0005 комбинированным методом корень уравнения x5–x–0.2=0 лежащий на интервале (1,1.1).
Определим, какой из концов отрезка выбрать в качестве начального приближения по методу хорд, и по методу касательных. Для этого вычислим f'(x)=5x4–1, f''(x)=20x3, f(1)f''(1)<0, значит положим x1=1 – начальное приближение по методу хорд, x2=1.1 – начальное приближение для метода касательных.
Program Komb; {комбинированный метод}
Const eps=0.0005;
Var
a,b,x,x1,x2,y1,y2,delta :Real;
n :Integer;
Function F(z:Real):Real;
Begin
F:=sqr(z)*sqr(z)*z-z-0.2;
End;
Function F1(z:Real):Real;
Begin
F1:=5*sqr(z)*sqr(z)-1;
End;
Function F2(z:Real):Real;
Begin
F2:=20*sqr(z)*z;
End;
Begin
Write ('Введите отрезок [a,b]-->');
ReadLn (a,b);
If F(a)*F2(a)<0 then begin x1:=a; x2:=b;
End
else begin x1:=b; x2:=a;
end;
n:=0;
Repeat
y1:=x1-F(x1)/(F(b)-F(x1))*(x2-x1);
y2:=x2-F(x2)/F1(x2);
delta:=abs(y2-y1);
n:=n+1;
x1:=y1; x2:=y2;
Until delta<eps;
x:=(x1+x2)/2.0;
WriteLn('Корень уравнения x=',x:8:4);
WriteLn('Проверка f(',x:8:4,')=',F(x):8:5);
WriteLn ('Количество приближений n=',n);
End.
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Для вычисления определенного интеграла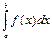 
используют квадратурные формулы вида
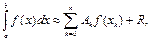
где xk и Ak определяются квадратурной формулой, R – остаточный член или погрешность квадратурной формулы.
Отрезок интегрирования [a,b] разбивается на n равных частей системой равноотстоящих точек xi=x0+ih, где i=0,1,2,...,n; x0=a, xn=b,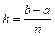 
— шаг разбиения. Затем вычисляем подынтегральную функцию в полученных узлах: yi=f(xi).
Квадратурные формулыдля равноотстоящих узлов:
1) формула левых прямоугольников:
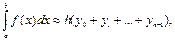где yi=f(xi), xi=a+ih;
2) формула правых прямоугольников:
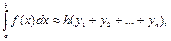где yi=f(xi), xi=a+ih;
3) формула центральных прямоугольников:
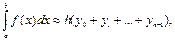где yi=f(xi),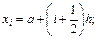 
4) формула трапеций:
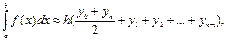где yi=f(xi), xi=a+ih;
5) формула Симпсона (формула парабол):
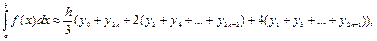
где yi=f(xi), xi=a+ih,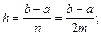 
6) формула Ньютона (правило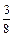 
):
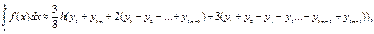
где yi=f(xi), xi=a+ih,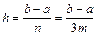 
.
Интегралы считаются с помощью квадратурных формул с точностью e. Для того, чтобы достичь требуемой точности вычисления e, используется способ двойного пересчета: интеграл вычисляют по выбранной квадратурной формуле дважды, сначала с некоторым шагом h, затем с шагом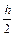 
, т.е. удваивают число n (количество точек разбиения [a,b]).
Обозначим результаты разбиений через Jn и J2n соответственно и сравним их. Если |Jn-J2n|<e, где e – погрешность вычислений, то в качестве результата берут J2n. Если |Jn-J2n|³e, то вычисления повторяют с шагом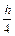 
и т.д.
Пример: С помощью формулы трапеций вычислить интеграл
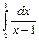с точностью e=0.01.
Program Integ1;
{Вычисление интеграла по формуле трапеций }
{без передачи имени функции в качестве параметра }
Uses Crt;
Const eps=0.01;
Var
a,b,eps,integral :Real;
nn :Integer;
{подинтегральная функция}
Function F(z:Real):Real;
Begin
f:=1/(z-1);
End;
{процедура вычисления интеграла}
Procedure Trap(a1,b1:Real; n:Integer;
eps1:Real; var tk:Real);
Var
i :Integer;
x,t0,s,h :Real;
Begin
t0:=f(a1)+f(b1)/2;
{t0–предыдущее значение интеграла}
{tk – последующее значение интеграла}
While True do
Begin
h:=(b1-a1)/n; {шаг}
s:=f(a1)+f(b1)/2;
For i:=1 to n-1 do
Begin
x:=a1+i*h;
s:=s+f(x);
end;
tk:=s*h;
If abs(tk-t0)<eps then Exit;
t0:=tk;
n:=2*n; {удваиваем количество разбиений}
end;
End;
Begin
Clrscr;
Write('Введите пределы интегрирования a,b’);
ReadLn (a,b);
nn:=6; {начальное значение количества разбиений}
Trap(a,b,nn,eps,integral);
WriteLn('Значение интеграла ',integral:8:4);
Repeat Until KeyPressed;
End.
{Вычисление интеграла по формуле трапеций }
{c передачей имени функции в качестве параметра }
Program Integ2;
Uses Crt;
Const eps=0.01;
Type Func=Function (z:Real):Real;
Var
a,b,eps,integral :Real;
nn :Integer;
{подинтегральная функция}
Function F1(z:Real):Real; Far;
Begin
F1:=1/(z-1);
end;
{процедура вычисления интеграла}
Procedure Trap(a1,b1:Real; n:Integer;
eps1:Real;f:Func; var tk:Real);
Var
I :Integer;
x,t0,s,h :Real;
Begin
t0:=f(a1)+f(b1)/2;
{t0 – предыдущее значение интеграла }
{tk – последующее значение интеграла}
While True do
Begin
h:=(b1-a1)/n; {шаг}
s:=f(a1)+f(b1)/2;
For i:=1 to n-1 do
Begin
x:=a1+i*h;
s:=s+f(x);
end;
tk:=s*h;
If abs(tk-t0)<eps then Exit;
t0:=tk;
n:=2*n; {удваиваем количество разбиений}
end;
End;
Begin
Clrscr;
Write('Введите пределы интегрирования a,b');
ReadLn (a,b);
nn:=6; {начальное значение количества разбиений}
Trap(a,b,nn,eps,F1,integral);
WriteLn('Значение интеграла ',integral:8:4);
Repeat Until KeyPressed;
End.
Дата добавления: 2015-04-15; просмотров: 1850;