Метод половинного деления

Для нахождения корня уравнения f(x)=0, принадлежащего отрезку [a,b], делим отрезок пополам, т.е. выбираем начальное приближение равным 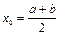. Если f(x₀)=0, то x₀ является корнем уравнения. Если f(x₀)¹0, то выбираем тот из отрезков [a,x₀] или [x₀,b], на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим те же рассуждения.

Процесс деления отрезков пополам продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданной точности e.

Пример: Методом половинного деления найти корень уравнения 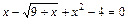на отрезке [2,3]с заданной точностью e=0.0001.

Program Poldel; {метод половинного деления}

Uses

Crt;

Const

eps=0.0001;

Var

x,a,b:Real;

Function F(z:Real):Real;

Begin

F:=z-sqrt(9+z)+z*z-4;

End;

Begin

Clrscr;

Write ('Ведите отрезок a,b -->');

ReadLn (a,b);

Repeat

x:=0.5*(b+a);

If f(x)=0 then Break;

If f(a)*f(x)<0 then b:=x

else a:=x;

Until b-a<eps;

WriteLn ('Корень уравнения x=',x:8:4);

WriteLn ('Проверка f(',x:8:4,')=',f(x):8:5);

Repeat Until KeyPressed;

End.