Метод итераций

Уравнение f(x)=0 представляем в виде x=j(x). Выбираем на отрезке [a,b] произвольную точку x₀ в качестве начального приближения и строим последовательность: x₁=j(x₀), x₂=j(x₁), ..., x_n=j(x_n-1). Процесс последовательного вычисления чисел x_n (n=1,2,3,...) называется методом итераций.

Если на отрезке [a,b] выполнено условие |j'(x)|≤q<1, то процесс итераций сходится, т.е. увеличивая n, можно получить приближение, сколь угодно мало отличающееся от истинного значения корня уравнения.

Процесс итераций продолжается до тех пор, пока не будет выполнено условие |x_n-x_n-1|£ 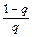e, где e — заданная точность вычислений. Если q≤0.5, то для прекращения процесса итераций можно пользоваться более простым соотношением |x_n-x_n-1|£e.

Геометрическая интерпретация метода итераций:

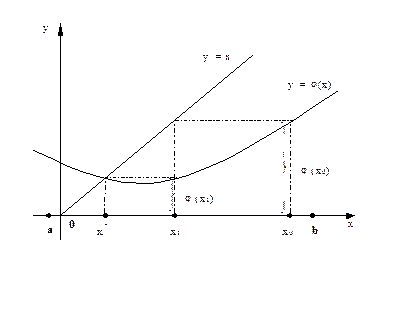
Пример: Методом итераций найти корень уравнения f(x)=arcsin(2x+1)-x²=0 расположенный на отрезке [-0.5,0] c точностью ε=10^-4.

Уравнение преобразуем к виду y=j(x) следующим образом:

arcsin(2x+1)=x², sin(arcsin(2x+1))=sin(x²), 2x+1=sin(x²), x=0.5(sin(x²)-1).

Значит j(x)= 0.5(sin(x²)-1), j^’(x)=xcos(x²), |j^’(x)|=|xcos(x²)|≤0.5 для xÎ[-0.5,0]. Метод итераций сходится.

Замечание: на каждом этапе необходимо помнить лишь два соседних приближения, поэтому приближение x_n обозначим через x, а приближение x_n+1через y.

Program Iter; {метод итераций}

Uses Crt;

Const eps=0.0001;

Var

fx,x,y,delta :Real;

n :Integer;

Function Fi(z:Real):Real;

Begin

Fi:=0.5*(sin(z*z)-1)

End;

Function F(z:Real):Real;

Begin

F:=2*z+1-sin(z*z);

End;

Begin

Clrscr;

Write ('Введите начальное приближение x=');

ReadLn (x);

n:=0;

Repeat

y:=Fi(x);

delta:=abs(y-x);

n:=n+1;

x:=y;

Until delta<eps;

WriteLn('Корень уравнения x=',x:8:4);

WriteLn('Проверка f(',x:8:4,')=',f(x):8:5);

WriteLn('Количество итераций n=',n);

Repeat Until KeyPressed;

End.