Метод Ньютона (касательных)

Пусть уравнение f(x)=0 имеет один корень на отрезке [a,b], причем f'(x) и f''(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [a,b].

Рассмотрим геометрическую интерпретацию этого метода. Возьмем некоторую точку x₀ отрезка [a,b] и проведем в точке P₀{x₀,f(x₀)} графика функции касательную к кривой y=f(x) до пересечения с осью Ox. Абсциссу x₁ точки пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку P₁{x₁,f(x₁)} и находя точку ее пересечения с осью Ox, получим второе приближение корня x₂. Аналогично определяются последующие приближения.

Выведем формулу для последовательных приближений к корню. Уравнение касательной, проходящей через точку P₀имеет вид:

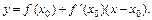
Полагая y=0, находим абсциссу x₁точки пересечения касательной с осью Ох: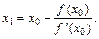

Следующие приближения находим по формулам: …, .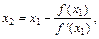

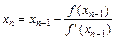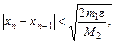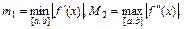Процесс вычислений прекращается при выполнении условия где Если 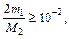то можно пользоваться более простым соотношением: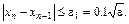

Для сходимости метода начальное приближение x₀ выбирают так, чтобы выполнялось условие f(x₀)f''(x₀)>0. В противном случае сходимость метода не гарантируется.

Пример: Методом Ньютона найти корень уравнения sin(x)-x+0.15=0на отрезке [0.5,1] c точностью ε=0.0001.

Найдем f'(x)=cos(x)–1, f''(x)=–sin(x). Расчетная формула имеет вид:

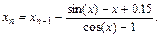
В качестве начального приближения возьмем x₀=1, т.к. f(1)f''(1)>0.

Вычислим m₁ и M₂: m₁=|cos(0.5)-1|=0.12, M₂=|-sin(1)|=0.84, значит

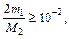и для проверки точности вычислений воспользуемся соотношением: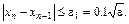

Замечание: На каждом этапе необходимо помнить лишь два соседних приближения, поэтому приближение x_n обозначим через x, а приближение x_n+1через y.

Program Kasat; {метод касательных }

Uses Crt;

Const

eps=0.0001;

Var

x,y,delta :Real;

n :Integer;

Function F(z:Real):Real;

Begin

F:=sin(z)-z+0.15;

End;

Function F1(z:Real):Real;

Begin

F1:=(cos(z)-1.0);

End;

Begin

Clrscr;

Write ('Введите начальное приближение x=');

ReadLn (x);

eps:=0.1*sqrt(eps);

n:=0;

Repeat

y:=x-F(x)/F1(x);

delta:=abs(y-x);

n:=n+1;

x:=y;

Until delta<eps;

WriteLn('Корень уравнения x=',x:8:4);

WriteLn('Проверка f(',x:8:4,')=',F(x):8:5);

WriteLn('Количество приближений n=',n);

Repeat Until KeyPressed;;

End.

Метод хорд

Пусть корень уравнения f(x)=0 лежит на отрезке [a,b]. Для определенности положим f(a)<0, f(b)>0.

Разделим отрезок [a,b] в отношении –f(a):f(b). Это дает приближенное значение корня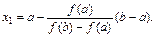

Далее применим этот прием к тому из отрезков [a,x₁] и [x₁,b] на концах которого функция f(x) имеет противоположные знаки, получим второе приближение корня x₂ и т.д.

Геометрически способ пропорциональных частей эквивалентен замене кривой y=f(x) хордой, проходящей через точки N{a,f(a)} и M{b,f(b)}.

Если конец b отрезка [a,b] неподвижен, то x₀=a и

;

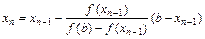если конец а отрезка [a,b] неподвижен, то x₀=b и

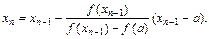
Процесс нахождения последовательных приближений продолжается до тех пор, пока не выполнится условие |x_n–x_n-1|£e. Для сходимости метода в качестве начального приближения нужно выбирать тот из концов отрезка, для которого выполняется условие f(x)f''(x)<0. Неподвижен тот конец отрезка, для которого f(x)f''(x)>0.

Геометрическая интерпретация метода хорд

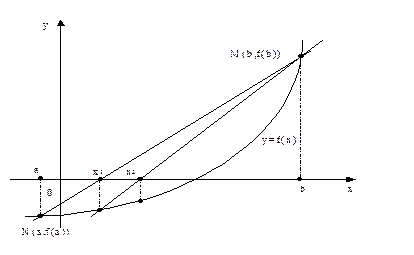Пример: Методом хорд найти корень уравнения x³–0.2x²–0.2x–1.2=0 расположенный на отрезке [1,2]c точностью ε=0.001.

Определим неподвижный конец f'(x)=3x²–0.4x–0.2, f''(x)=6x–0.4, f(2)f''(2)>0значит неподвижной будет точка x=2, в качестве начального приближения возьмем x=1.

Замечание: На каждом этапе необходимо помнить лишь два соседних приближения, поэтому приближение x_n обозначим через x, а приближение x_n+1через y.

Program Xord; {метод хорд}

Const eps=0.001;

Var

x,y,delta :Real;

n :Integer;

Function F(z:Real):Real;

Begin

F:=z*z*z+0.2*z*z-0.2*z-1.2;

End;

Begin

Write ('Введите начальное приближение x=');

ReadLn (x);

n:=0;

Repeat

y:=x-F(x)/(F(b)-F(x))*(b-x);

delta:=abs(y-x);

n:=n+1;

x:=y;

Until delta<eps;

WriteLn('Корень уравнения x=',x:8:4);

WriteLn('Проверка f(',x:8:4,')=',F(x):8:5);

WriteLn('Количество приближений n=',n);

End.