Подстановка (3.56) в (3.57) дает простейший вид уравнения Лапласа
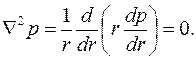
|
Общим решением этого уравнения является функция
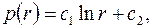
| (3.58) |
где 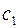 и
и 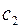 – постоянные интегрирования, определяемые граничными условиями (3.55).
– постоянные интегрирования, определяемые граничными условиями (3.55).
В результате получим решение первой основной граничной задачи фильтрации (3.55 – 3.57):
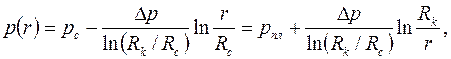
| (3.59) |
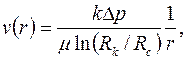
| (3.60) |
где 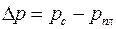 – заданный перепад давления между скважиной и пластом.
– заданный перепад давления между скважиной и пластом.
При поглощении 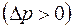 проявлении
проявлении 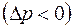 пласта объемный расход жидкости через любую цилиндрическую поверхность
пласта объемный расход жидкости через любую цилиндрическую поверхность 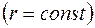 , в том числе и через стенку скважины,
, в том числе и через стенку скважины,
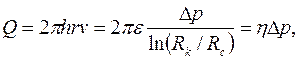 - формула Дюпюи - формула Дюпюи
| (3.61) |
где 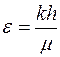 ;
; 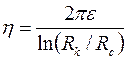 – соответственно коэффициент гидропроводности, или просто гидропроводность, и коэффициент продуктивности, или просто продуктивность пласта; размерность м3/Па.с.
– соответственно коэффициент гидропроводности, или просто гидропроводность, и коэффициент продуктивности, или просто продуктивность пласта; размерность м3/Па.с.
Формула (3.61) впервые получена французским инженером Дюпюи и поэтому названа его именем.
Дата добавления: 2015-03-07; просмотров: 856;
