Которое впервые было получено Л. С. Лейбензоном в 1930г.

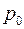Наиболее известный приближенный метод решения этого уравнения основан на линеаризации, по Л. С. Лейбензону, который состоит в том, что левую часть уравнения умножают на , а правую – на некоторое характерное давление , например давление в невозмущенной части пласта.

Тогда вместо (2.60) необходимо решить линейное уравнение

,

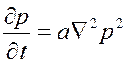(2.61)

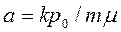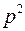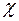которое аналогично уравнению (2.33), где . Следовательно, все соотношения, полученные до сих пор для жидкости, могут быть в первом приближении использованы и при изучении фильтрации газа, если заменить в них на , на .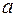

Лекция 4. 5. Экспериментально установлено, что иногда линейный закон фильтрации жидкости 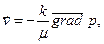(2.58) нарушается и зависимость между 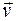и 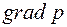принимает вид выпуклой или вогнутой кривой, как показано на рис. 11.

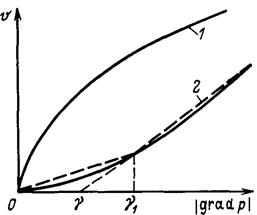
Рис. 11.Возможные виды нелинейного закона фильтрации

Основные причины проявления нелинейных эффектов следующие:

а) высокая скорость фильтрации, когда параметр Рейнольдса 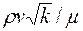превышает критическое значение (зависимость изображена кривой 1 на рис. 11);

б) ламинарная фильтрация жидкостей с неньютоновскими свойствами (кривая 2);

в) малая скорость фильтрации в слабопроницаемых и неоднородных пластах (кривая 2).

Предложены различные аппроксимации нелинейных зависимостей. Например, кривая 1 чаще всего описывается двучленным законом фильтрации

,

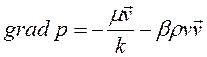(2.62)

а кривая 2 – законом фильтрыции с предельным градиентом

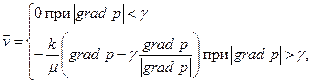
(2.63)

где, по данным Е. М. Минского, 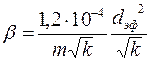, а, по данным Б. И. Султанова, 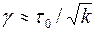; 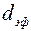- эффективный диаметр пор; 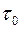- предельное напряжение сдвига.

В общем случае к обоим типам кривых применимы степенная и кусочно-линейная аппроксимации

,

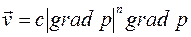(2.64)

,

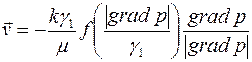(2.65)

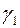которыми удобно пользоваться при расчетах. Здесь - параметры модели; - характерное значение градиента давления; 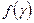- безразмерная функция, описывающая ломаную линию (см. рис. 11).