При жестком режиме фильтрации или при установившейся фильтрации уравнение (2.54) обращается в уравнение Лапласа (2.34).
Следовательно, ставить задачу о фильтрации жидкости в трещиновато-пористой среде имеет смысл при 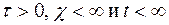 .
.
Начальное и граничные условия, которые необходимо присоединить к уравнению (2.54), обладают некоторой особенностью. Прежде всего ясно, что граничную задачу, связанную с уравнением (2.54) следует рассматривать относительно одного из давлений – 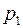 или
или 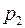 .
.
Если начальные условия 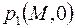 и
и 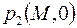 удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления
удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления 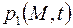 , принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления
, принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления 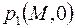 вычисляют поровое давление
вычисляют поровое давление 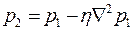 .
.
В противном случае задачу следует решать относительно давления 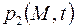 . Но здесь имеет место определенная специфика в задании граничных условий.
. Но здесь имеет место определенная специфика в задании граничных условий.
Если начальное распределение давления 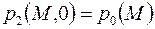 согласовано с граничными условиями
согласовано с граничными условиями 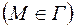 вида
вида
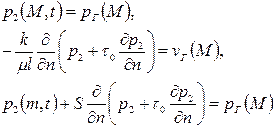 , ,
| (2.55) |
при 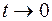 , то в таком виде граничная задача и рассматривается.
, то в таком виде граничная задача и рассматривается.
Но если же согласования нет, то к правым частям соответствующих граничных условий необходимо прибавить слагаемое 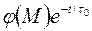 , где
, где 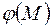 – невязка существующего граничного условия:
– невязка существующего граничного условия:
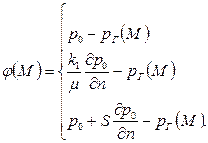
| (2.56) |
Это свидетельствует о том, что заданный скачок граничных условий в порах трещиновато-пористой среды не уничтожается мгновенно, как в обычной пористой среде, а убывает по закону 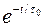 . Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений
. Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений 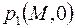 и
и 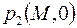 .
.
После решения граничной задачи относительно порового давления 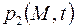 распределение давления
распределение давления 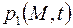 в трещинах определяется по формуле (2.53)
в трещинах определяется по формуле (2.53)
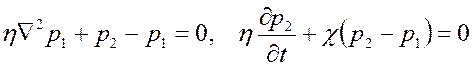
Дата добавления: 2015-03-07; просмотров: 1200;
