Несовершенное вскрытие пластов
Фильтрация, отличная от плоско-радиальной, возникает и в том случае, когда пласт вскрыт не на всю мощность, а частично или часть пласта перекрыта обсадной колонной, или связь пластовой и скважинной жидкостей осуществляется через перфорационные отверстия в колонне.
В этих случаях говорят о несовершенном вскрытии пласта и задают граничное условие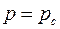 
лишь на открытой части поверхности 
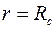, а на остальной условие непроницаемости 
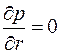. Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется.
Известны различные приближенные аналитические решения этих задач и экспериментальные исследования на моделях, учитывающие тот или иной вид несовершенства вскрытия пласта.
Общий вывод, который следует из полученных решений, сводится к тому, что расход жидкости и в этих случаях вычисляется по обобщенной формуле Дюпюи (3.49), где приведенный радиус скважины
 ,
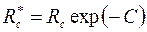| (3.90) |
здесь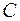 
– показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта.
Отношение расхода жидкости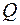 
при несовершенном вскрытии к расходу 
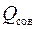при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)]
коэффициент сопротивления:
| (3.91) |
.
В общем случае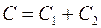 
где 
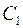и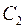 
– показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта 
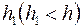Маскет, используя метод источников, нашел, что при 
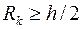показатель несовершенства по степени вскрытия можно определить по формуле
| (3.91) |
.
Здесь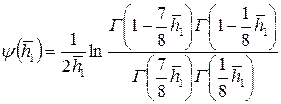 
,
где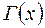 
– гамма-функция (известная, табулированная функция); 
.
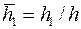Представление о функции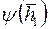 
и показателе 
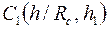дает табл. 3.
Таблица 3
| 
| |||||||
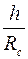
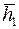
| 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | |
| ||||||||
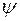
| 0,43 | 0,84 | 1,38 | 2,04 | 2,93 | 4,33 | 7,1 | 13,11 | |
| 0,16 | 0,47 | 0,91 | 1,52 | 2,35 | 2,62 | 5,35 | 8,1 | |
| 0,24 | 0,65 | 1,21 | 1,98 | 3,04 | 3,65 | 6,87 | 10,87 | |
| 0,41 | 1,05 | 1,89 | 3,05 | 4,66 | 6,07 | 10,63 | 17,39 | |
| 0,49 | 1,22 | 2,19 | 3,52 | 5,35 | 7,11 | 12,24 | 20,08 |
Например, при Rc = 0,1 м, h = 20 м, h1 = 10 м, согласно таблице при h/Rc=200 и h1=0,5, получим С1=3,35, что при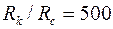 
соответствует коэффициенту сопротивления КС = 0,65.
Существенное значение в этой задаче могут иметь различные проницаемости вдоль пласта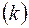 
и в направлении, перпендикулярном к пласту 
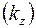, т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта 
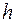приведенной 
.
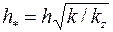Если, например,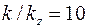 
, то по данным предыдущего примера имеем 
, 
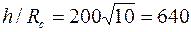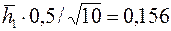и, согласно формулам, 
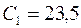и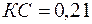 
.
Несовершенство по характеру вскрытия имеет место, когда связь со скважиной осуществляется через круглые или щелевые отверстия в обсадной колонне. В этом случае показатель несовершенства может быть вычислен по следующим приближенным формулам:
| (3.93) |
где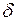 
– открытая часть поверхности колонны; 
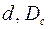– диаметры перфорационных отверстий и скважины; т — число рядов щелей.
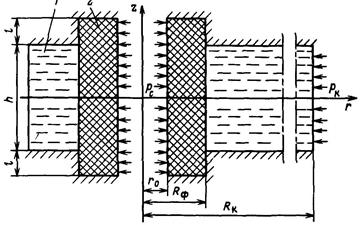
Рис. 3.5 Схема призабойной зоны скважины с искусственным фильтром
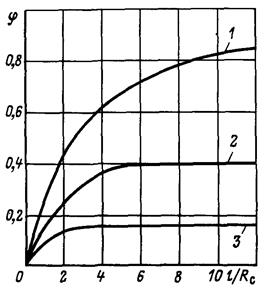
Рис. 3.6 Зависимость показателя снижения фильтрационного сопротивления от величины дополнительной зоны фильтрации при h/Re = 15: 1 2, 3 соответственно при Rф/Rc = 8; 5; 3.
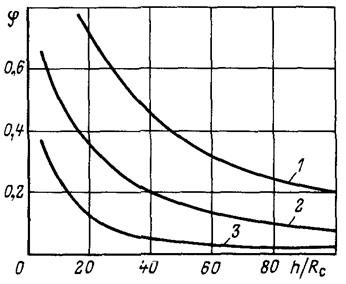
Рис. 3.7Зависимость показателя снижения фильтрационного сопротивления от мощности пласта и радиуса фильтра приl/Rф = 2: 1, 2, 3 соответственно
при Rф/Rc = 8; 5; 3
Приведем решение задачи, когда приствольная зона скважины оборудована искусственным фильтром (2)высотой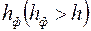 
и проницаемостью 
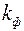, отличной от проницаемости пласта (1)(рис. 3.5).
Приведенный радиус в этом случае
 ,
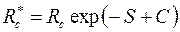| (3.94) |
где 
– параметр «скин-эффекта» [см. формулу (3.71)];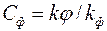 
показатель снижения сопротивления, обусловленный наличием дополнительной зоны 
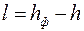; φ – функция безразмерных параметров 
, 
, 
.
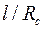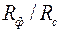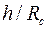На рис. 3.6 показаны графики зависимости φ от 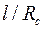при трех значениях отношения 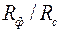и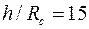 
. Из него следует, что с увеличением 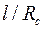функция 
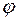быстро растет до асимптотического значения, которое наступает при 
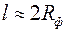. Это доказывает нецелесообразность установки фильтра высотой больше чем 
.
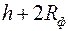Влияние мощности пласта на φиллюстрируется графиками на рис.3.7 при тех же значениях 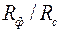и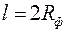 
.
Лекция 5
Дата добавления: 2015-03-07; просмотров: 1053;
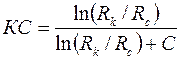
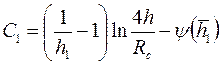