Следовательно, искомая напряженность будет равна
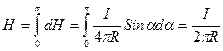(8)
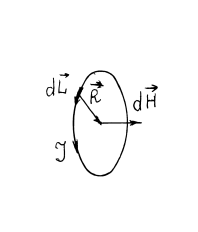Направление вектора H находят по правилу буравчика. Располагают его жало вдоль проводника. Вращение рукоятки должно вызвать перемещение буравчика в направлении протекания тока. Направление вращения концов рукоятки совпадает с направлением вектора напряженности в данной точке (Рис.4).
|
|
. Тогда, согласно формуле (6), для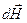 
имеем
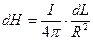. (9)
|
H найдем интегрированием выражения (9) вдоль контура.
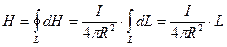(10)
где L - длина контура. Так как контур - окружность, то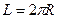 
. Тогда для H получим
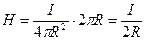(11)
Важной характеристикой поля является циркуляция вектора, представляющего собой силовую характеристику поля. Циркуляцией вектора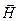 
по контуру L называют интеграл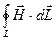 
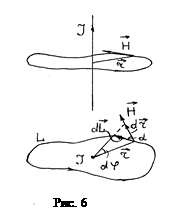
Вычислим циркуляцию напряженности 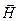магнитного поля, созданного прямым проводником с током, по контуру L (рис.4). Контур лежит в плоскости перпендикулярной проводнику и охватывает этот проводник. Вид на рассматриваемый контур представлен на рис. 6б.
Согласно формуле (6) 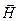лежит в плоскости контура и для скалярного произведения 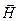на 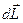( 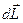-вектор перемещения вдоль контура), в соответствии с рис.6б, имеем 
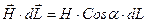. Напряженность поля H, созданного в данной точке пространства бесконечным прямым проводником с током I равна.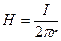 
Следовательно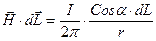 
Согласно рис. 6б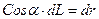 
, так как в случае малости 
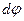, dL можно рассматривать как гипотенузу, а dr как катет прямоугольного треугольника. В этом приближении (малость угла 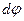) dr является дугой окружности радиуса r, на которую опирается центральный угол 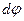и, следовательно, 
.
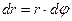С учетом сказанного, для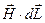 
получим
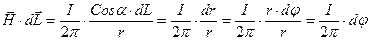
и циркуляция вектора 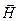вдоль замкнутого контура, охватывающего проводник с током, будет равна 
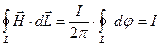(12)
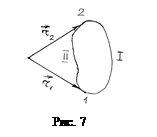так как, при движении вдоль контура, радиус-вектор совершит полный оборот, и приращение угла будет равно 2 
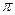. Если контур не охватывает проводник с током, то приращение угла j равно 0 , так как при движении из точки 1 в точку 2 по части контура 1 имеем положительное приращение угла (рис.7), а при движении из точки 2 в точку 1 по части контура II отрицательное. В результате в сумме получим 0. Выражение (12) получено нами в предположении, что контур лежит в плоскости, перпендикулярной проводнику с током, а проводник прямой. Однако можно показать, что оно справедливо при произвольной ориентации контура относительно проводника и произвольной форме проводника. Если контур охватывает несколько проводников с током, то под I следует понимать алгебраическую сумму токов всех проводников, охватываемых контуром. При этом ток считается положительным, если вектор 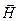, созданного им поля, совпадает с направлением обхода контура и отрицательным в противном случае.
Таким образом, циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна полной силе тока, протекающего сквозь поверхность, ограниченную рассматриваемым контуром(закон Полного тока). Силовые поля, для которых циркуляция силовой характеристики поля отлична от нуля, называют вихревыми. Магнитное поле, в отличие от электростатического, является вихревым.
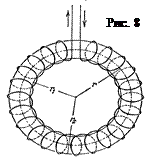
В ряде случаев выражение (12) удобно использовать для расчета характеристик полей проводников сложной конфигурации. Применим формулу (12) для нахождения напряженности поля тороидальной катушки (рис.8). Из соображений симметрии следует, что напряженность поля одинакова во всех точках окружности, центр которой совпадает с центром тороида. Выберем такую окружность в качестве контура интегрирования.
Очевидно, что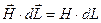 
и, так как H=const , вдоль выбранного контура, то
.
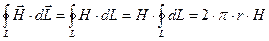Полный ток через площадь, ограниченную контуром, очевидно, будет равен NI, где N – число витков тороидальной катушки. Следовательно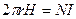 
, откуда
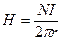(13)
Поле тороида неоднородно. У внутренней границы его напряженность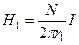 
, а у внешней 
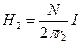. Их относительная разность равна 
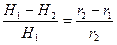. Устремим радиус тороидальной катушки в бесконечность. В этом случае 
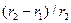стремится к нулю и 
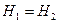. Следовательно, поле такой катушки будет однородным. Отрезок окружности очень большого радиуса можно рассматривать как отрезок прямой, следовательно, любой отрезок тороида в случае, когда r стремится к бесконечности, можно рассматривать как прямую катушку. Такую катушку называют соленоидом. В формуле (13) 
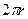- длина тороидальной катушки, отношение же 
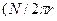) = n это число витков, приходящееся на единицу длины. Следовательно, соленоид создает однородное магнитное поле, напряженность которого равна
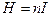(14)
Мы рассмотрели поля, создаваемые проводниками и контурами различной формы. Вернемся к рассмотрению вопроса о силовом действии магнитного поля на элемент тока в этом поле.
Согласно формуле (1) на элемент тока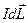 
в магнитном поле с индукцией 
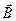действует сила 
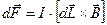, которую называют силой Ампера. По сути своей это результирующая сил действующих со стороны магнитного поля на движущиеся в проводнике носители зарядов. Получим из формулы (1) выражение для силы, действующей на движущуюся заряженную частицу. Для этого представим 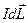в следующем виде:
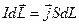(15)
Здесь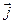 
- плотность тока, а S – площадь поперечного сечения проводника. Считаем, что 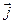во всех точках сечения проводника одинакова.
Плотность тока 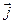находится по формуле:
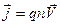(16),
где V– средняя скорость направленного движения носителей зарядов в проводнике, n – их плотность, q – заряд носителя.
Подставим (16) в формулу (1) для силы, получим
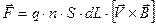. (17)
Но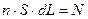 
- полное число носителей зарядов в рассматриваемом элементе проводника dL . Следовательно, сила 
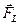, действующая на носитель заряда,движущийся в проводнике, будет равна 
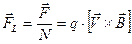. (18)
Эта сила носит название силы Лоренца. Мы получили выражение для нее в предположении, что заряженные частицы (носители зарядов) движутся в проводнике. Очевидно, что для проявления действия этой силы на движущуюся заряженную частицу наличие проводника необязательно. Сила действует на любую заряженную частицу, движущуюся в магнитном поле в направлении, отличном от направления вектора .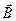
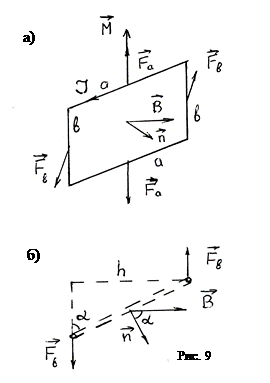
Рассмотрим поведение замкнутого контура с током в однородном магнитном поле (рис. 9а). Контур представляет собой прямоугольную рамку. (Рис. 9б вид на контур сверху). На рис.9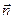 
- единичный вектор к плоскости контура. Направление его выбираем так, чтобы из конца вектора мы видели ток, текущим против часовой стрелки. Силы 
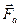, действующие на стороны a контура, равны по величине и противоположно направлены. Они могут вызвать только деформацию контура. Силы 
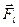образуют пару сил, вызывающих вращение контура вокруг некоторой оси. Они стремятся развернуть контур так, чтобы плоскость его стала перпендикулярно к вектору 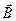. Вращающий момент 
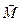пары направлен по оси вращения, а величина его равна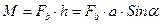 
Так как согласно (1)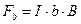 
, то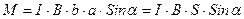 
Здесь учтено, что площадь S , ограниченная контуром, равна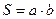 
.
В соответствии со схемой рис.9а это выражение можно представить в векторном виде.
.
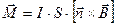Вводя в рассмотрение вектор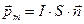 
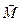для , получим 
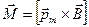. (19)
Вектор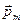 
называют магнитным моментом контура с током. Направление его определяют по правилу буравчика. Вращают рукоятку буравчика по направлению протекания тока в контуре. Направление перемещения буравчика при вращении определит направление вектора 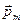к плоскости, ограниченной контуром.
Мы получили выражение для 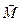в случае прямоугольного контура. В действительности эта формула справедлива для контуров с током произвольной формы. Таким образом, на контур с током в магнитном поле действует вращающий момент, стремящийся развернуть его таким образом, чтобы вектор магнитного момента контура 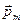совпал по направлению с вектором 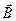. Ориентирующее действие магнитного поля на контур с током позволяет использовать его для нахождения направления вектора 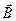в данной точке пространства. Все сказанное справедливо не только для контуров с током, но и для постоянных магнитов, которым также можно приписать некоторый магнитный момент. Ориентирующее действие магнитного поля Земли на магнитную стрелку использовано в данной работе для нахождения горизонтальной составляющей напряженности магнитного поля Земли.
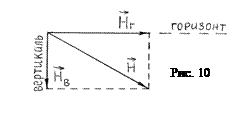Земля имеет магнитное поле. Вектор напряженности 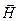этого поля в любой точке пространства может быть разложен на горизонтальную 
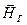и вертикальную 
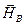составляющие (рис.10). На горизонтально расположенную стрелку с магнитным моментом 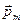в магнитном поле Земли действует вращающий момент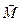
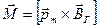(20),
где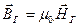 
- горизонтальная составляющая вектора магнитной индукции магнитного поля Земли (для воздуха 
).
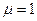Магнитная стрелка поворачивается в магнитном поле Земли до тех пор, пока ее направление не совпадет с направлением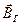 
.
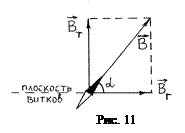Тангенс-гальванометром называют круговой проводник, в центре которого расположена магнитная стрелка. Расположим тангенс-гальванометр так, чтобы плоскость витка совпадала с направлением стрелки, и подключим его к источнику тока. Стрелка будет находиться не только в магнитном поле Земли, но и в поле кругового тока, и установится в направлении вектора 
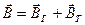(рис.11). Так как 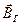перпендикулярен 
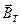, то
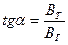(21)
С учетом формул (4) и (11) индукция магнитного поля в центре N витков кругового тока радиусом R равна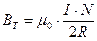 
(22)
Тогда для горизонтальной составляющей вектора индукции и напряженности магнитного поля Земли соответственно имеем
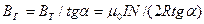(23)
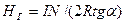(24)
Измерив силу тока I и угол отклонения магнитной стрелки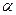 
и зная число и радиус витков кругового тока, можно экспериментально определить горизонтальную составляющую индукции и напряженности магнитного поля Земли. Если же известно из предыдущих измерений значение горизонтальной составляющей H или B магнитного поля Земли, то, определив экспериментально угол отклонения магнитной стрелки, при помощи описанного устройства можно оценить величину тока
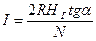(25),
которая прямо пропорциональна тангенсу угла отклонения магнитной стрелки. Отсюда и происходит название используемого в работе прибора «тангенс-гальванометр». Коэффициент пропорциональности перед tg 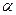в формуле (25) называют постоянной тангенс-гальванометра
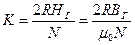(26)
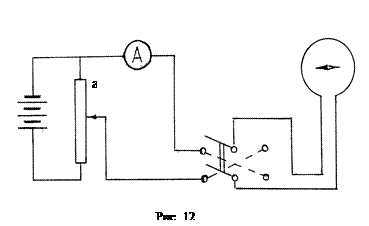Описание установки.
Для выполнения работы собрать электрическую цепь из источника тока, потенциометра, переключателя на два положения, амперметра и тангенс-гальванометра в соответствии с рис.12. Переключатель в данной работе позволяет изменять направление тока в витках. Число витков и радиус витков приведены в надписях к прибору.
Порядок выполнения работы:
1. Установить тангенс-гальванометр так, чтобы его магнитная стрелка оказалась в плоскости круговых витков.
2. Собрать электрическую цепь в соответствии с рис.12. Движок реостата установить в положение а.
3. Изменяя величину тока при помощи потенциометра, определить углы отклонения магнитной стрелки от первоначального положения при 5 значениях силы тока (указываются преподавателем). Изменить положение переключателя и повторить измерения.
4. Результаты измерений записать в таблицу и вычислить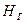 
и 
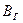по формулам (23) и (24) для каждого значения силы тока, используя средние значения углов отклонения.
5. Вычислить постоянную тангенс-гальванометра по формуле (26), взяв среднее значение .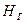
6. Вычислить абсолютную ошибку для каждого из измерений по формуле
.
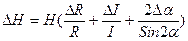
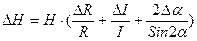и результаты занести в таблицу.
7. Вычислить средние значения 
| №№ п/п | Величина тока I,А | Угол отклонения в градусах | tg a | Hг, А/м | DНг, А/м | Вг=m0Нг, Тл | ||
| Вправо | Влево | Средний | ||||||
| Средние значения |
Для получения зачета изучить следующие теоретические вопросы:
1.Понятие о магнитном поле.
2.Магнитный момент контура с током.
3.Поведение контура с током в магнитном поле.
4.Силовые характеристики магнитного поля. Магнитная проницаемость среды.
5.Сила Лоренца.
6.Сила Ампера.
7. Закон Био-Савара-Лапласа. Принцип суперпозиции полей.
8.Закон полного тока.
9.Напряженность и индукция магнитного поля прямого тока и в центре кругового тока.
10.Магнитное поле тороида и соленоида.
ЛИТЕРАТУРА.
1. И.В.Савельев. Курс общей физики, т.2, п.п. 39-41, 1977.
2. И.В.Савельев. Курс общей физики, т.2,п.п.40,42-44, 1982.
3. Г.А.Зисман, О.М.Тодес. Курс общей физики, т.2, п.п.29,32, 1974.
4. В.М.Яворский, А.А.Детлаф, Л.Б.Милковская. Курс физики, т.2, гл.14.1, 14.2, 15.1, 15.2, 15.4, 15.5, 1977.
Лабораторная работа №9
Дата добавления: 2015-03-07; просмотров: 1804;