ФИЗИЧЕСКИЕ ОСНОВЫ РАБОТЫ ПОЛУПРОВОДНИКОВЫХ ДИОДОВ И ТРИОДОВ
Все твердые тела по их способности проводить электрический ток делятся на три категории: проводники, полупроводники и изоляторы (диэлектрики). Удельное сопротивление проводников порядка 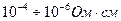 , проводников
, проводников 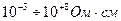 , а диэлектриков
, а диэлектриков 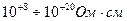 .
.
Электропроводность твердых тел объясняется в современной физике на основе зонной теории твердых тел. Чтобы понять происхождение зон рассмотрим воображаемый процесс объединения атомов в кристалл. Согласно квантовой теории энергия электронов в атоме квантуется. Это значит, что она может принимать лишь дискретные значения, называемые также энергетическими уровнями, т.е. каждый электрон обладает одним из разрешенных значений энергии, занимая при этом один из дозволенных энергетических уровней.
Энергетические уровни в одном изолированном атоме представлены схематически на рис.1а. Рассмотрим теперь N одинаковых атомов, изолированных друг от друга. Энергетические уровни системы N невзаимодействующих атомов представлены на рис. 1б. В отсутствии взаимодействия они одинаковы у каждого атома и такие же, как у изолированного атома.
 |
Теперь будем сближать атомы друг с другом, чтобы они образовали кристаллическую решетку. Тогда из-за взаимодействия между атомами разрешенные значения энергии в каждом из них станут различными, и каждый уровень изолированного атома расщепиться на N близко расположенных уровней
(рис. 1в), образуя, таким образом, разрешенную энергетическую зону. Виду того, что N очень велико, расстояния между уровнями одной и той же зоны крайне малы, так что требуется ничтожная энергия, чтобы перевести электрон в пределах зоны с одного энергетического уровня на другой. Разрешенные энергетические зоны разделены запрещенными энергетическими зонами, они разделяют разрешенные энергетические зоны, и в запрещенных зонах нет разрешенных значений энергий электронов.
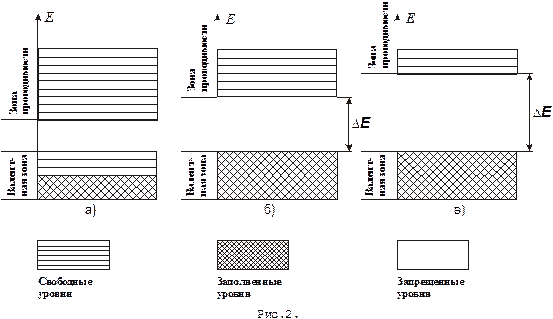
У разных веществ взаимное расположение разрешенных зон и их заполнение электронами различно, и этим определяются их свойства. Интерес представляют те энергетические зоны, которые заполняются электронами в последнюю очередь. На рис. 2. изображены три возможных случая заполнения валентных зон электронами, соответствующих металлам (а), полупроводникам (б), диэлектрикам (в).
На этом рисунке нижняя зона представляет собой валентную зону, которая у полупроводников и диэлектриков при температурах, близких к абсолютному нулю, полностью заполнена электронами. Металлы имеют или частично заполненную валентную зону или полностью заполненную, но перекрывающуюся с выше расположенной зоной со свободными энергетическими уровнями. И в том и другом случае валентная зона, заполняемая электронами, имеет свободные энергетические уровни, как это показано на рис. 2(а). При этом электроны в металлах могут участвовать в механизме электропроводности вне зависимости от температуры, так как возникновение электрического тока означает переход электронов, создающих электрический ток, на более высокие уровни, а это возможно в металлах при любых температурах (есть выше расположенные свободные энергетические уровни в заполняемой энергетической зоне). Валентную зону в металлах, в которой имеются свободные энергетические уровни, не заполненные электронами, называют зоной проводимости.
В полупроводниках заполненная электронами валентная зона отделена от незаполненной зоны возбужденных уровней конечным интервалом энергий DE рис. 2(б). В полупроводниках свободную валентную, расположенную над заполненной, по аналогии с металлами называют зоной проводимости. При абсолютном нуле температур валентная зона полностью заполнена электронами, а зона проводимости полностью свободна (пуста). Поэтому при абсолютном нуле полупроводники не проводят электрического тока, т.е. являются изоляторами. Изоляторы отличаются от полупроводников только большими значениями ширины запрещенной зоны DE рис. 2(в). Условно к изоляторам относят те полупроводники, для которых DE превосходит примерно 2 эВ. Никакого качественного различия между полупроводниками и изоляторами нет. Различие чисто количественное.
При повышении температуры электроны начинают обмениваться энергией с ионами кристаллической решетки. Благодаря этому электрон может получить добавочную кинетическую энергию порядка kT. Этой энергии может оказаться достаточно, чтобы некоторые электроны перевести из валентной зоны в зону проводимости. Такие электроны, перейдя в зону проводимости, начинают проводить электрический ток, так как в этой зоне есть свободные выше расположенные уровни. Но проводимость возникает и по другой причине. В валентной зоне освобождаются квантовые состояния, не занятые электронами, на которые могут перемещаться электроны с нижних уровней, при этом освобождается ниже расположенный уровень. Получается, что не занятое квантовое состояние перемещается к дну энергетической зоны. Такие квантовые состояния получили название дырок. Дырки также являются носителями электрического тока.
В чистых полупроводниках число электронов и дырок одинаково. Оба эти типа носителей заряда дают вклад в электропроводность полупроводника, ее называют собственной электропроводностью в отличие от примесной электропроводности, обусловленной наличием примесей атомов других химических элементов.
Чаще всего используют два полупроводниковых кристалла: кремний и германий.
Атом кремния имеет три электронные оболочки. Четыре электрона внешней (третьей), незаполненной оболочки являются валентными, они участвуют во взаимодействиях между атомами, образуя кристаллы кремния. Внешняя оболочка кремния имеет четыре вакантных состояния, которые могут быть заняты электронами других атомов. Эти вакансии и обеспечивают формирование кристаллической решетки (рис. 3); каждый атом взаимодействует с четырьмя соседними благодаря ковалентным (парно электронным) связям и этим как бы дополняет внешнюю оболочку до восьми электронов.
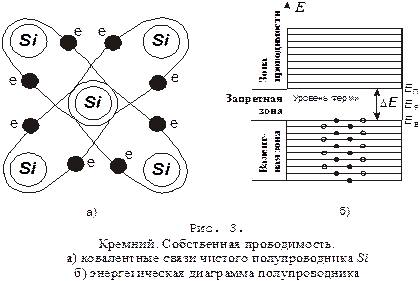 На основании изложенного выше можно объяснить механизм электропроводности чистого полупроводника. При сообщении кристаллу некоторого количества энергии отдельные электроны, энергия которых увеличилась более чем на DE, перейдут из валентной зоны в зону проводимости. Это означает, что эти электроны разорвали связь со своими парами атомов и стали свободными. При этом в зоне проводимости появляется некоторое количество носителей тока – электронов, занимающих уровни вблизи дна зоны. При приложении внешнего электрического поля они придут в упорядоченное движение, создавая электрический ток. В энергетическом представлении это означает их переход в зоне проводимости на более высокие уровни. Одновременно с образованием свободных электронов в валентной зоне освобождается такое же число мест на верхних уровнях - дырок. Появление дырки означает образование в кристаллической решетке положительного иона кремния после отрыва одного из электронов, осуществлявшего ковалентную связь (точнее, происходит частичная ионизация пары соседних атомов). Поэтому дырке приписывается положительный заряд, равный по абсолютному значению заряду электрона. Таким образом, в чистом полупроводнике при нарушении ковалентной связи возникает пара носителей заряда – электрон и дырка (рис. 3б).
На основании изложенного выше можно объяснить механизм электропроводности чистого полупроводника. При сообщении кристаллу некоторого количества энергии отдельные электроны, энергия которых увеличилась более чем на DE, перейдут из валентной зоны в зону проводимости. Это означает, что эти электроны разорвали связь со своими парами атомов и стали свободными. При этом в зоне проводимости появляется некоторое количество носителей тока – электронов, занимающих уровни вблизи дна зоны. При приложении внешнего электрического поля они придут в упорядоченное движение, создавая электрический ток. В энергетическом представлении это означает их переход в зоне проводимости на более высокие уровни. Одновременно с образованием свободных электронов в валентной зоне освобождается такое же число мест на верхних уровнях - дырок. Появление дырки означает образование в кристаллической решетке положительного иона кремния после отрыва одного из электронов, осуществлявшего ковалентную связь (точнее, происходит частичная ионизация пары соседних атомов). Поэтому дырке приписывается положительный заряд, равный по абсолютному значению заряду электрона. Таким образом, в чистом полупроводнике при нарушении ковалентной связи возникает пара носителей заряда – электрон и дырка (рис. 3б).
Если поместить кристалл в электрическое поле, то свободные (находящиеся в зоне проводимости) электроны начнут перемещаться в сторону, противоположную направлению поля, обеспечивая упорядоченный перенос зарядов, т.е. электрический ток. При этом вакантные места (дырки) будут перемещаться в направлении поля за счет того, что электрон от соседнего атома перескакивает на вакантное место, двигаясь против поля, что соответствует перемещению положительно заряженного места в кристаллической решетке (дырки) в направлении поля. Таким образом, дырки, как и электроны, участвуют в создании электрического тока в полупроводниках. Здесь уместно обратить внимание на разницу в переносе зарядов ионами и дырками. В электролите или газе ионизированный атом движется сам. В кристалле полупроводника атом неподвижен; лишь поочередная ионизация неподвижных атомов имитирует движение дырки.
Кроме полупроводников с собственной проводимостью, существуют полупроводники с примесной проводимостью. Примесный полупроводник образуется за счет дефектов кристалла, доноров или акцепторов. Эти дефекты являются результатом внедрения в кристаллическую решетку атомов химических элементов, валентность которых превосходит валентность полупроводника или уступает ей. Их соответственно называют донорными или акцепторными примесями.
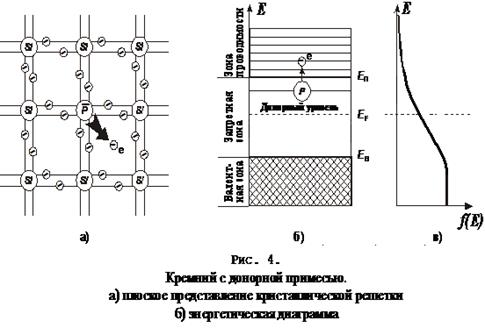
Для кремния донорными примесями обычно служат элементы группы периодической системы – фосфор /Р/ или сурьма /Sb/. Атом донорной примеси образует ковалентную связь с четырьмя соседними атомами кремния посредством четырех валентных электронов, пятый же валентный электрон становиться лишним, его связь с атомом ослабляется: при весьма низкой температуре он занимает энергетический уровень в запрещенной зоне, вблизи границы с зоной проводимости, однако уже при незначительном нагревании этот электрон переходит в зону проводимости (рис. 4а).
Количество свободных электронов оказывается равным сумме атомов донорной примеси и «собственных» электронов, перешедших в зону проводимости в результате разрушения ковалентной связи.
Т.к. электропроводность в рассмотренном случае будет в основном определяться электронами, то их называют основными носителями заряда в противовес дыркам, называемым в этом случае не основными носителями. Такой примесный проводник называется электронным или полупроводник n-типа (от латинского слова negative, т.е. отрицательный); говорят также, что такой полупроводник обладает электронным видом проводимости.
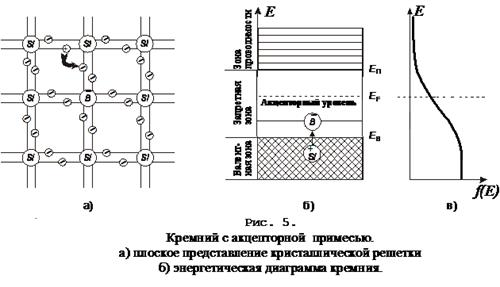
Для кремния акцепторными примесями обычно служат элементы III группы периодической системы, - алюминий /Al/, бор /B/, галий /Ga/. Атому акцепторной примеси для образования ковалентной связи с четырьмя соседними атомами кремния в дополнение к трем валентным электронам нужен четвертый (рис. 5а).
Соответствующий вакантный энергетический уровень находиться в запрещенной зоне, вблизи границы валентной зоны. При незначительном нагреве на этот уровень из валентной зоны перейдет электрон; возникает ион кремния, т.е. образуется «дырка». В этом случае дырки как «примесные», так и «собственные» называются основными носителями, а электроны – не основными. Такой примесный полупроводник называют дырочным или полупроводник р-типа (от латинского positive – положительный); говорят также, что такой полупроводник обладает дырочной проводимостью.
Наряду с образованием носителей тока – генерацией носителей в полупроводнике одновременно идет процесс их рекомбинации. При данной температуре скорости генерации и рекомбинации равны: имеет место термодинамическое равновесие.
Уровень Ферми в полупроводниках имеет тот же смысл, что и в металлах. В чистом полупроводнике уровень Ферми EF располагается приблизительно в середине запрещенной зоны. У полупроводников с донорной примесью уровень Ферми смещается вверх относительно его положения чистом полупроводнике, а в случае акцепторной примеси – вниз (см. рис.4 и рис.5).
 |
Рассмотрим кратко температурную зависимость электропроводимости твердых тел.
Удельная электропроводность определяется выражением: 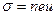
где: n – концентрация, e – заряд, u – подвижность носителей тока.
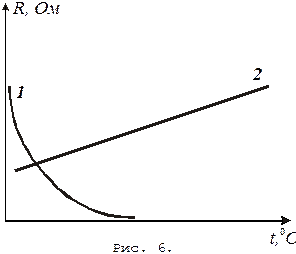
В металлах, как уже отмечалась, повышение температуры практически не увеличивает концентрации электронов проводимости, зато уменьшает их подвижность. Это ведет к уменьшению электропроводности 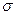 и соответственно к увеличению сопротивления
и соответственно к увеличению сопротивления  металлов с ростом температуры (рис. 6).
металлов с ростом температуры (рис. 6).
В отличие от металлов концентрация свободных электронов в чистых полупроводниках при увеличении температуры растет по экспоненциальному закону и может быть выражена формулой:
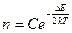 , (1)
, (1)
где: DE – ширина запрещенной зоны, k – константа Больцмана, Т – абсолютная температура, C – константа.
Подвижность электронов убывает с понижением температуры, однако гораздо медленнее резкого увеличения концентрации свободных электронов n. Поэтому без большой ошибки можно считать, что для чистых полупроводников:
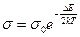 (2)
(2)
где: 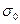 - некоторая константа.
- некоторая константа.
Если полупроводник имеет примеси, то в общем случае электропроводность выражается формулой: 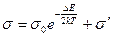 (3)
(3)
Первый член уравнения (3) обозначает собственную проводимость полупроводника; второй член – примесную проводимость. При низких температурах собственная проводимость практически равна нулю и температурная зависимость проводимость полупроводника определяется в основном проводимостью примеси. С повышением температуры большую роль начинает играть собственная проводимость. При температуре 300-400K примесные уровни почти полностью ионизируются, и температурная зависимость проводимости полупроводника определяется лишь собственной проводимостью. В области температур, где решающую играет собственная проводимость, зависимость проводимости полупроводников от температуры определяется формулой (2), а сопротивление 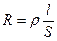 , где
, где 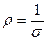 - формулой:
- формулой: 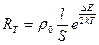 . Обозначая
. Обозначая 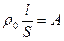 и
и 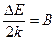 , получим:
, получим: 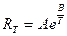
Зависимость сопротивления от температуры для полупроводника (1) и металла (2) показана на рис. 6.
Контактные явления. В основе работы многих полупроводниковых приборов лежат электрические явления, происходящие при контакте электронного и дырочного полупроводников или металла и дырочного полупроводника. При наличии контакта между n-полупроводником и р-полупроводником, электроны из n-полупроводника диффундируют в р-полупроводник, где концентрация электронов значительно меньше, и рекомбинируют с электронами. Электрическая нейтральность полупроводника нарушается: в n-полупроводнике, вблизи контакта появляется пространственный положительный заряд, а в р-полупроводнике – отрицательный заряд, т.е. в тонком пограничном слое толщиной 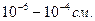 появляется контактное электрическое поле EK (рис. 7). Контактное поле препятствует перетеканию зарядов вследствие диффузии. Помимо электронов в n-полупроводнике и дырок в p-полупроводнике, являющихся основными носителями электрических зарядов для этих полупроводников, в них присутствуют и неосновные носители. В n-полупроводнике это дырки, а в p-полупроводнике – электроны. Их появление связано с рождением пар электрон-дырка, обуславливающих собственную проводимость полупроводников. Возникающее контактное электрическое поле с напряженностью
появляется контактное электрическое поле EK (рис. 7). Контактное поле препятствует перетеканию зарядов вследствие диффузии. Помимо электронов в n-полупроводнике и дырок в p-полупроводнике, являющихся основными носителями электрических зарядов для этих полупроводников, в них присутствуют и неосновные носители. В n-полупроводнике это дырки, а в p-полупроводнике – электроны. Их появление связано с рождением пар электрон-дырка, обуславливающих собственную проводимость полупроводников. Возникающее контактное электрическое поле с напряженностью 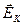 не является для них препятствием. Под действием этого поля неосновные носители придут в движение, создавая ток проводимости jE. При определенном значении EK диффузионный ток
не является для них препятствием. Под действием этого поля неосновные носители придут в движение, создавая ток проводимости jE. При определенном значении EK диффузионный ток 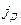 уравновешивается встречным током проводимости
уравновешивается встречным током проводимости 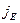 и в полупроводниках устанавливается равновесие.
и в полупроводниках устанавливается равновесие. 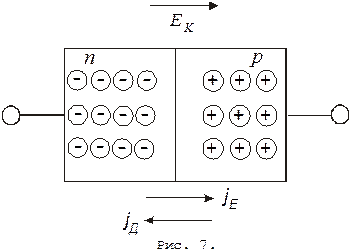 В состоянии равновесия
В состоянии равновесия 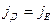 . Сказанное иллюстрирует рис. 8а, соответствующий условию равновесия. На этом рисунке изображены две энергетические оси: на левой оси откладывается энергия электронов, на правой – энергия дырок. Энергетическая ось дырок направлена вниз, из чего следует, что энергия дырок в n-области выше, чем в р-области. Ток проводимости
. Сказанное иллюстрирует рис. 8а, соответствующий условию равновесия. На этом рисунке изображены две энергетические оси: на левой оси откладывается энергия электронов, на правой – энергия дырок. Энергетическая ось дырок направлена вниз, из чего следует, что энергия дырок в n-области выше, чем в р-области. Ток проводимости 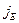 через в р-n-переход является током неосновных носителей, скатывающихся с энергетического барьера. Его величина определяется концентрацией неосновных носителей, которая очень незначительна. Диффузионный ток
через в р-n-переход является током неосновных носителей, скатывающихся с энергетического барьера. Его величина определяется концентрацией неосновных носителей, которая очень незначительна. Диффузионный ток 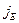 через в р-n переход обусловлен основными носителями, но только теми, энергия которых достаточна для преодоления энергетического барьера. Поэтому величина
через в р-n переход обусловлен основными носителями, но только теми, энергия которых достаточна для преодоления энергетического барьера. Поэтому величина 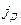 зависит от высоты энергетического барьера, чем ниже барьер, тем больше число электронов и дырок смогут его преодолеть и наоборот.
зависит от высоты энергетического барьера, чем ниже барьер, тем больше число электронов и дырок смогут его преодолеть и наоборот.
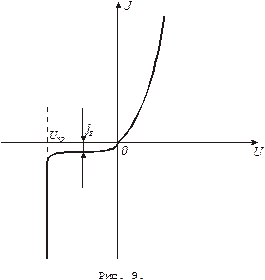
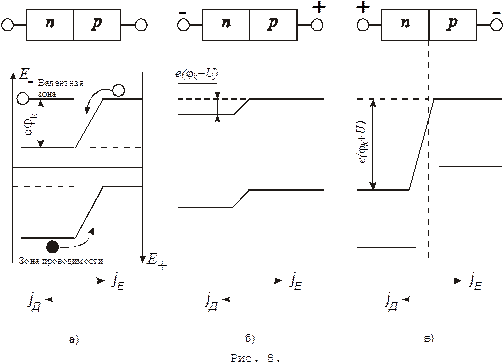 |
Предположим, что к р-n переходу, находившимся в равновесии, приложено в прямом направлении внешнее электрическое поле (т.е. к n-области подключен отрицательный полюс источника, а к р-области – положительный, рис. 8б. U – разность потенциалов между концами полупроводлников). Т.к. внешнее поле не совпадает по направлению с собственным контактным полем, то высота энергетического барьера уменьшиться до
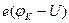 . При этом ток проводимости
. При этом ток проводимости 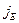 , величина которого не зависит от высоты энергетического барьера, останется неизменным. Диффузионный же ток
, величина которого не зависит от высоты энергетического барьера, останется неизменным. Диффузионный же ток 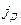 возрастает. В результате через р-n-переход пойдет ток, равный практически диффузионному току и величина его будет быстро расти с увеличением приложенного напряжения.
возрастает. В результате через р-n-переход пойдет ток, равный практически диффузионному току и величина его будет быстро расти с увеличением приложенного напряжения.
Приложим теперь к р-n-переходу внешнее напряжение U в обратном направлении (рис. 8в). Т.к. внешнее поле теперь совпадает по направлению с собственным контактным полем, то высота энергетического барьера возрастает до 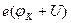 . Ток проводимости при этом так же, как и в первом случае, останется неименным, а диффузионный ток уменьшиться. В результате полный ток через р-n переход будет практически равен току проводимости, который является током неосновных носителей и поэтому весьма мал. Вольт-амперная характеристика (ВАХ) р-n-перехода представлена на рис. 9.
. Ток проводимости при этом так же, как и в первом случае, останется неименным, а диффузионный ток уменьшиться. В результате полный ток через р-n переход будет практически равен току проводимости, который является током неосновных носителей и поэтому весьма мал. Вольт-амперная характеристика (ВАХ) р-n-перехода представлена на рис. 9.
Нелинейный вид ВАХ свидетельствует о том, что в р-n-переходе образуется запирающий слой, обладающий односторонней проводимостью. Из рис. 9. видно, что обратный ток в определенных пределах остается постоянным, а при некотором значении обратного напряжения он резко возрастает. Наступает электрический пробой p-n перехода. Напряжение, при котором это наблюдается, называется пробивным.
СНЯТИЕ ВОЛЬТ-АМПЕРНОЙ ХАРАКТЕРИСТИКИ И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КРИССТАЛЛИЧЕСКОГО ДИОДА.
Принадлежности: диод германиевый, миллиамперметр, микроамперметр, потенциометр, вольтметр, переключатель.
 Описание метода и установки. Полупроводниковые диоды изготовляются обычно из германия или кремния и могут быть точечными или плоскостными в зависимости от того, в точке или плоскости происходит контакт двух областей с разным типом проводимости.
Описание метода и установки. Полупроводниковые диоды изготовляются обычно из германия или кремния и могут быть точечными или плоскостными в зависимости от того, в точке или плоскости происходит контакт двух областей с разным типом проводимости.
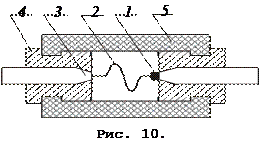
На рис. 10. приведена схема точечного германиевого диода. Точечный контакт осуществляется между пластиной Ge-1 и вольфрамовой пружиной 2, которые, с помощью кристаллодержателей 3 и металлических фланцев 4 укреплены в керамическом корпусе 5.
Полупроводниковые диоды применяются для выпрямления переменного тока, в технике СВЧ, импульсной технике и имеют различное устройство и параметры в зависимости от своего назначения.
 Вольт-амперная характеристика (ВАХ) диода (т.е. зависимость тока от напряжения) показана на рис. 9. Она состоит из двух ветвей: для прямого напряжения и обратного. Для наглядности прямая и обратная ветви вычерчены в разном масштабе, поскольку прямой ток измеряется в миллиамперах, а обратный – в микроамперах.
Вольт-амперная характеристика (ВАХ) диода (т.е. зависимость тока от напряжения) показана на рис. 9. Она состоит из двух ветвей: для прямого напряжения и обратного. Для наглядности прямая и обратная ветви вычерчены в разном масштабе, поскольку прямой ток измеряется в миллиамперах, а обратный – в микроамперах.
 Детектирующие свойства кристаллического диода характеризуются коэффициентом выпрямления:
Детектирующие свойства кристаллического диода характеризуются коэффициентом выпрямления: 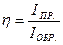 при
при 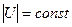 (4),
(4),

 где
где 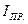 ;
; 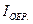 - прямой и обратный токи.
- прямой и обратный токи.

 Другой параметр кристаллического диода – величина внутреннего сопротивления
Другой параметр кристаллического диода – величина внутреннего сопротивления 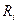 в направлении пропускания тока:
в направлении пропускания тока:


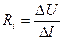 (5)
(5)
Измерения:
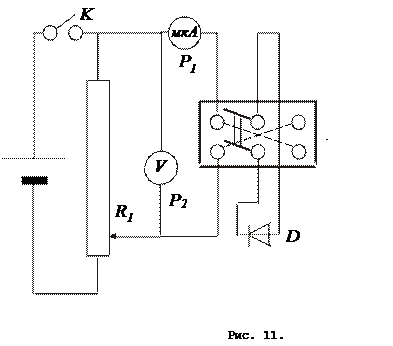
1. Собирают схему (рис. 11).
2. Снимают ВАХ диода в прямом направлении. Для этого увеличивают напряжение от 0 до 2В через 0,2В и для каждого значения напряжения измеряют с помощью миллиамперметра величину тока.
3. Снимают ВАХ в обратном направлении. Для этого выбирают наименьший предел измерения миллиамперметра и переключателем меняют знак прикладываемого к диоду напряжения. Изменяют напряжение в пределах 0-12В через 1В и отмечают показания приборов.
4. Результаты измерений заносят в таблицу 1.
Таблица 1
| Прямое напряжение, В | Прямой ток, мА | Обратное напряжение, В | Обратный ток, мкА |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2 1,4 1,6 1,8 2,0 |
5. Строят ВАХ диода (в разном масштабе для прямого и обратного токов).
6. Используя график ВАХ, определяют внутреннее сопротивление диода при различных значениях прямого напряжения. Для этого разбивают ось напряжений на интервалы, находят по графику соответствующие приращения тока и по формуле (5) рассчитывают 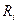 . Вычисленное значение
. Вычисленное значение 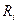 относят к среднему значению напряжения в интервале. Составляют таблицу значений
относят к среднему значению напряжения в интервале. Составляют таблицу значений 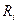 в функции U.
в функции U.
Таблица 2
| № п/п | U, В | DU, В | DI, мА | 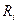 , Ом , Ом
| 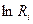
| |
7. Строят график зависимости сопротивления –р-n-перехода от прямого напряжения в линейном и полулогарифмическом масштабе.
Для получения зачета необходимо проработать следующие вопросы:
1. Нарисовать и объяснить структуру энергетических зон в металлах, полупроводниках и диэлектриках.
2. Что такое собственная проводимость полупроводников?
3. Каков механизм образования примесной проводимости?
4. Чем отличается дырочная проводимость от электронной?
5. Что такое уровень Ферми и каково его расположение в чистых и примесных полупроводниках?
6. Как зависит от температуры сопротивление металла, собственного полупроводника, примесного полупроводника?
7. Какие физические процессы происходят при контакте двух полупроводников с разным типом проводимости?
8. Что такое запирающий слой и как он возникает?
Литература.
1. И.В.Савельев. Курс физики, «Наука»,1989 г. т.III.,§41-43
2. Д.В.Сивухин. Общий курс физики, т.III., Электричество,§100
ЛАБОРАТОРНАЯ РАБОТА N 8
ИЗМЕРЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ НАПРЯЖЕННОСТИ
МАГНИТНОГО ПОЛЯ ЗЕМЛИ С ИСПОЛЬЗОВАНИЕМ ТАНГЕНС-ГАЛЬВАНОМЕТРА
Цель работы:
1. Изучить теоретический материал по теме: Магнитное поле Земли.
2. Оценить величину горизонтальной составляющей напряженности и индукции магнитного поля Земли в районе г. Москвы.
3. Определить постоянную тангенс-гальванометра, используемого в работе.
Теоретическое введение.
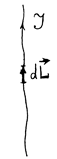 Проводники с током взаимодействуют между собой. Причиной взаимодействия является появление вокруг проводников с током силового поля, называемого магнитным. Так как ток это направленное движение зарядов, то источником магнитного поля являются движущиеся заряды. Из взаимодействия проводников с током следует, что на движущиеся в этом поле заряды (проводники с током) действуют силы.
Проводники с током взаимодействуют между собой. Причиной взаимодействия является появление вокруг проводников с током силового поля, называемого магнитным. Так как ток это направленное движение зарядов, то источником магнитного поля являются движущиеся заряды. Из взаимодействия проводников с током следует, что на движущиеся в этом поле заряды (проводники с током) действуют силы.
 При рассмотрении взаимодействия проводников с током вводят понятие "элемент тока", которое в законах магнитного взаимодействия играет ту же роль, что понятие точечного заряда в законах электрического взаимодействия. Под "элементом тока" понимают произведение
При рассмотрении взаимодействия проводников с током вводят понятие "элемент тока", которое в законах магнитного взаимодействия играет ту же роль, что понятие точечного заряда в законах электрического взаимодействия. Под "элементом тока" понимают произведение 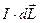 , где I - сила тока, текущего по проводнику, а вектор
, где I - сила тока, текущего по проводнику, а вектор 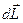 - элемент проводника длиной
- элемент проводника длиной  dL, направленный вдоль тока (рис. 1).
dL, направленный вдоль тока (рис. 1).
Результаты опытов по исследованию взаимодействия проводников с током можно сформулировать следующим образом. На элемент тока 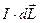 , находящийся в магнитном поле, созданном проводником с током, действует сила, величина и направление которой определяется некоторым вектором
, находящийся в магнитном поле, созданном проводником с током, действует сила, величина и направление которой определяется некоторым вектором 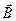 , характеризующим магнитное поле, созданное проводником с током в точке пространства, где находится элемент тока
, характеризующим магнитное поле, созданное проводником с током в точке пространства, где находится элемент тока 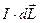 . При этом сила, действующая на этот элемент равна
. При этом сила, действующая на этот элемент равна 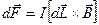 (1)
(1)
Вектор B называется магнитной индукцией и является силовой характеристикой магнитного поля. Соотношение (1) дает определение магнитной индукции и является математическим выражением закона, установленного Ампером. Наряду с магнитной индукцией для описания магнитного поля вводят другую физическую величину H, называемую напряженностью магнитного поля. Связь между ними в случае изотропных магнитных свойств окружающей среды следующая
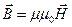 (2),
(2),
 где
где 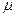 - относительная магнитная проницаемость среды, показывающая во сколько раз значение
- относительная магнитная проницаемость среды, показывающая во сколько раз значение 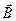 в среде отличается от его значения в вакууме. Очевидно, что в вакууме
в среде отличается от его значения в вакууме. Очевидно, что в вакууме
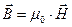 . (3)
. (3)
Знание 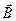 необходимо для нахождения силы, действующей на проводник с током в магнитном поле. В то время как
необходимо для нахождения силы, действующей на проводник с током в магнитном поле. В то время как 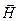 удобно использовать при расчете магнитных полей, создаваемых проводниками с током различной конфигурации, так как
удобно использовать при расчете магнитных полей, создаваемых проводниками с током различной конфигурации, так как 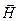 не зависит от магнитных свойств окружающей среды.
не зависит от магнитных свойств окружающей среды.
Для магнитного поля справедлив принцип суперпозиции. Согласно этому принципу магнитная индукция 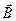 поля, созданного несколькими проводниками с током, равна векторной сумме магнитных индукций
поля, созданного несколькими проводниками с током, равна векторной сумме магнитных индукций 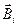 полей, созданных каждым из проводников. Это же справедливо и в отношении вектора напряженности поля
полей, созданных каждым из проводников. Это же справедливо и в отношении вектора напряженности поля 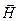 . Таким образом
. Таким образом
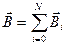
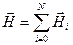 (4),
(4),
где N - число проводников с током.
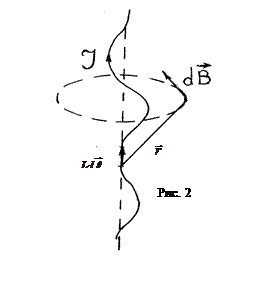
Отсюда можно заключить, что магнитную индукцию или напряженность поля, создаваемую контуром или проводником с током, можно найти, суммируя магнитные индукции (напряженности) от отдельных элементов, на которые можно разбить данный контур или проводник. Для решения подобной задачи необходимо иметь выражение для индукции или напряженности поля, созданного элементом тока 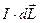 . Формула для магнитной индукции поля, создаваемого элементом тока
. Формула для магнитной индукции поля, создаваемого элементом тока 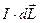 была получена Био, Саваром, Лапласом и носит название закона Био-Савара-Лапласа. Она имеет следующий вид :
была получена Био, Саваром, Лапласом и носит название закона Био-Савара-Лапласа. Она имеет следующий вид :
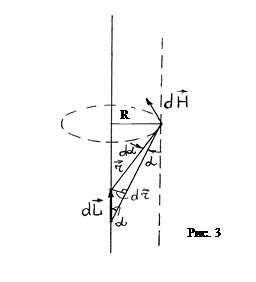
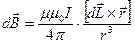 , (5)
, (5)
где 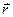 - вектор, проведенный от элемента ток в ту точку, в которой определяется вектор магнитной индукции
- вектор, проведенный от элемента ток в ту точку, в которой определяется вектор магнитной индукции 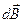 (см. рис.2), r - модуль этого вектора. Остальные величины, входящие в формулу (5), были определены ранее. В соответствии с выражением (3) для напряженности поля получим формулу
(см. рис.2), r - модуль этого вектора. Остальные величины, входящие в формулу (5), были определены ранее. В соответствии с выражением (3) для напряженности поля получим формулу
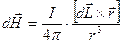 . (6)
. (6)
Используем формулу (6) для нахождения напряженностей полей двух типов проводников: бесконечного прямого проводника и кругового проводника.
Рассмотрим бесконечный прямой проводник с током. Хотим найти напряженность поля 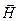 в точке отстоящей от него на расстоянии R. Разобьем проводник на элементы тока. Напряженность поля проводника в данной точке, согласно принципу суперпозиции, равна векторной сумме напряженностей полей, созданных каждым из этих элементов. В соответствии с формулой (6) вектор
в точке отстоящей от него на расстоянии R. Разобьем проводник на элементы тока. Напряженность поля проводника в данной точке, согласно принципу суперпозиции, равна векторной сумме напряженностей полей, созданных каждым из этих элементов. В соответствии с формулой (6) вектор 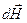 поля любого из элементов тока будет перпендикулярен плоскости, в которой лежит проводник и интересующая нас точка пространства. Следовательно, все
поля любого из элементов тока будет перпендикулярен плоскости, в которой лежит проводник и интересующая нас точка пространства. Следовательно, все 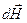 направлены одинаково, и сложение векторов можно заменить сложением их модулей. Суммирование эквивалентно интегрированию. Следовательно,
направлены одинаково, и сложение векторов можно заменить сложением их модулей. Суммирование эквивалентно интегрированию. Следовательно, 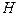 будет равна интегралу от dH вдоль проводника. Согласно (6)
будет равна интегралу от dH вдоль проводника. Согласно (6)
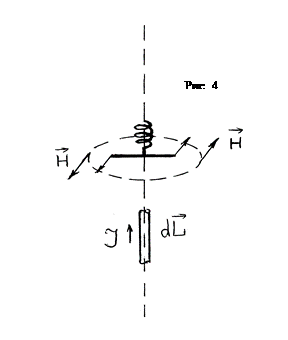
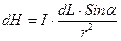 (7)
(7)
В соответствии с рис.3 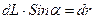 есть длина дуги окружности радиуса r, на которую опирается центральный угол da. Следовательно
есть длина дуги окружности радиуса r, на которую опирается центральный угол da. Следовательно 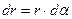 , в свою очередь
, в свою очередь  .
.
Из этого следует, что 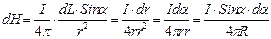
Таким образом, от переменной L мы перешли к переменной 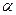 . Интеграл вдоль проводника означает интегрирование по новой переменной в пределах от 0 до
. Интеграл вдоль проводника означает интегрирование по новой переменной в пределах от 0 до 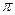 .
.
Дата добавления: 2015-03-07; просмотров: 1660;
