Переход к теоретическому познанию

Большой объем эмпирических знаний был накоплен древними цивилизациями Востока. И в Китае, и в Вавилоне, и в Египте были достаточно развиты математика и астрономия, и была подмечена повторяемость, регулярность в небесных и вообще природных явлениях. Однако переход на следующий, теоретический уровень знания был осуществлен лишь в Древней Греции.

Известны вавилонские и египетские учебники математики. Они представляют собой сборники задач с конкретными числовыми условиями, и решениями, выполненными по принципу: сначала вычитаем, потом делим, потом прибавляем — вот и ответ. Почему именно так? — никаких общих правил или доказательств нет, да и само понятие доказательства было незнакомо математике Древнего Востока. В этом отношении такие «учебники» мало отличаются от сборника магических заклинаний или поваренной книги.

Первым известным нам человеком, который от решения конкретных вычислительных задач перешел к доказыванию общих теоретических утверждений, был грек Фалес Милетский (VII–VI вв. до н.э.). Фалес доказывал, что всякий круг делится диаметром пополам, а всякий угол,

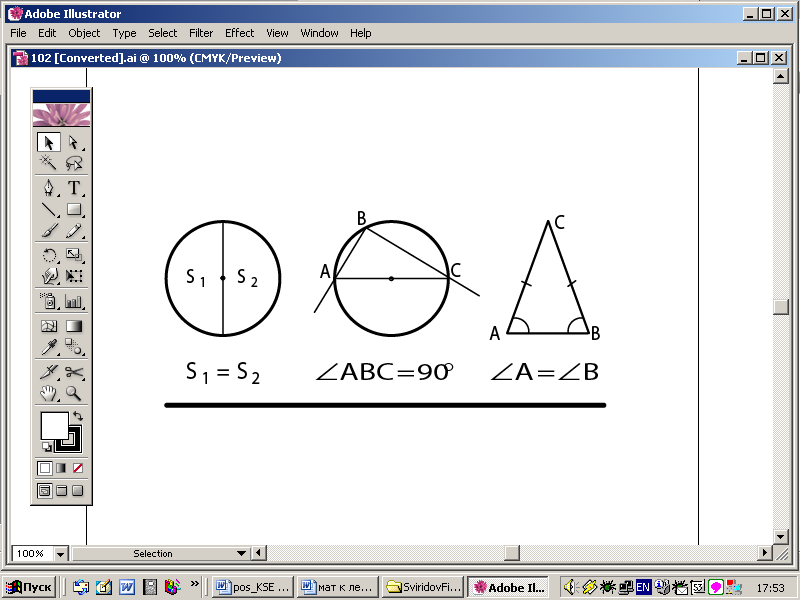
опирающийся на диаметр — прямой, что углы при основании всякого равнобедренного треугольника равны¼

Можно нарисовать тысячи разных кругов, и все они будут делиться своими диаметрами строго пополам. Дает ли это уверенность, что диаметр делит пополам всякий круг, круг вообще? Нет, уверенность может дать только общее доказательство, оперирующее не с конкретными кругами, а с абстракцией круга.

Абстракции позволяют упрощать картину явления и рассматривать его как бы в «чистом виде». Они возникают в результате абстрагирования.

Абстрагирование — метод познания, основанный на том,
что не учитываются несущественные стороны и признаки изучаемого явления.

Основной абстракцией Фалеса и его учеников стало представление о единой субстанции, лежащей в основе мира, — материи. Основа миропорядка сводилась к качественным изменениям этой субстанции, которые и объясняли возникновение, развитие и структуру окружающего мира.

У самого Фалеса роль субстанции еще играло конкретное вещество — вода, однородная, бесформенная и подвижная, а у его ученика Анаксимена — воздух. Однако другой ученик Фалеса, Анаксимандр, уже учил, что первоосновой сущего служит апейрон («беспредельное»), не воспринимаемый непосредственно органами чувств.

С развитием метода абстрагирования стали одна за другой создаваться абстракции все более высокого уровня. Дистанция между ними и их корнями в реальности вскоре возросла настолько, что абстракции в представлении некоторых греческих философов приобрели самостоятельную реальность, порой рассматривавшуюся как первичная по отношению к реальности чувственного мира. Такой, например, стала абстракция числа в трактовке школы Пифагора. «Всё есть число», — утверждал Пифагор. Числа, с его точки зрения, представляют собой самостоятельные сущности, являющиеся первоосновой мира.

Пифагорейцы заложили основы дедуктивного метода.

Дедукция —метод познания, основанный на выведении частных следствий из общих посылок.

Греческие мыслители поняли, что соблюдение определенных правил гарантирует получение правильных выводов из правильного исходного положения. Совокупность правил мышления оформилась в отдельную философскую дисциплину — логику. Легендарный Аристотель (384–322 гг. до н.э.) сформулировал основные законы логики и ввел понятие элементарного умозаключения (силлогизма). Силлогизм, по Аристотелю, состоит из двух исходных положений (посылок) и выводимого из них заключения. Например, из посылок «Все люди смертны» и «Сократ — человек» вытекает, что Сократ смертен.

Не все силлогизмы доказательны. Так, например, из посылок «Сократ — человек» и «Сократ — грек» не следует, что все люди — греки. Аристотель классифицировал типы (модусы) силлогизмов и указал среди них работающие («правильные»). Кроме того, он сформулировал критерии истинности суждений (п. 0). Действительно, что дает нам основание утверждать, что все люди смертны или что Сократ — человек?