Уравнения гиперболического типа
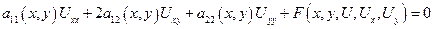
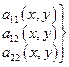 – заданные функции
– заданные функции
F – известная функция
U(x,y) – исходная функция, удовлетворяющая уравнению
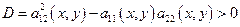
для 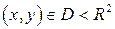 – гиперболическая
– гиперболическая
D = 0, то параболическая
D < 0, то эллиптическая
Сделаем замену: 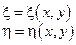 ,
,
то уравнение перепишется:
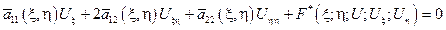
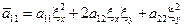
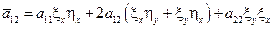
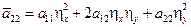
1-ый случай:
Приведение к каноническому виду квазилинейный уравнений 2-ого порядка гиперболического типа.
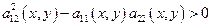 для любых
для любых 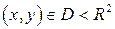
Рассмотрим дифференциальное уравнение:
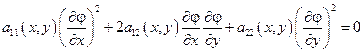
Если 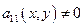 , то решим его как обычное квадратное уравнение относительно отношения
, то решим его как обычное квадратное уравнение относительно отношения
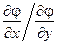 – получим систему 2-х уравнений
– получим систему 2-х уравнений
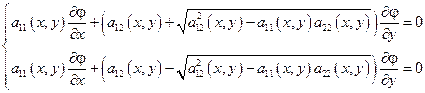
Для интегрирования системы составим систему обыкновенных дифференциальных уравнений.
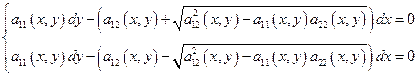
Решения этих 2-х уравнений и будут исходными решениями исходного уравнения.
Последнюю систему можно написать в виде одного уравнения:
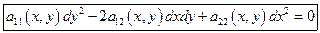
Уравнение – характеристическое уравнение исходного квазилинейного уравнения.
И решение его 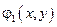 и
и 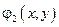 таковы, что
таковы, что
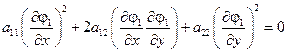
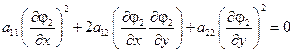
Если выбрать 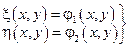 , то
, то 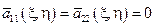 .
.
Причем 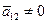 и канонический вид гиперболического уравнения будет следующим:
и канонический вид гиперболического уравнения будет следующим:
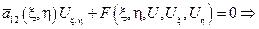
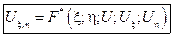 канонический вид уравнения гиперболического типа.
канонический вид уравнения гиперболического типа.
Пример:
Привести к каноническому виду уравнение гиперболического типа:
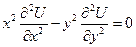 .
.
Решение:
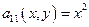
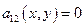
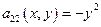
Определим тип уравнения => найдем дискриминант этого уравнения:
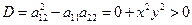 , если x ≠ 0 и y ≠ 0.
, если x ≠ 0 и y ≠ 0.
Уравнение является гиперболическим почти во всей плоскости, кроме x = 0 или y = 0 (оси).
Напишем характеристическое уравнение исходного уравнения:
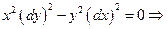
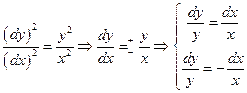
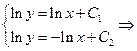
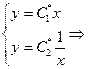
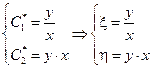
Найдем произведение Uxx и Uyy, участвующие в исходном уравнении через новые переменные:
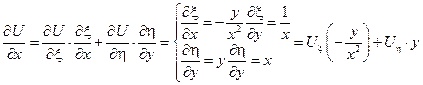
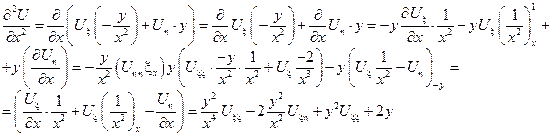
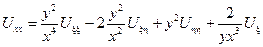
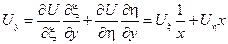
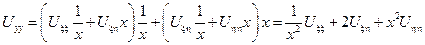
Подставим найденные производные в исходное уравнение:
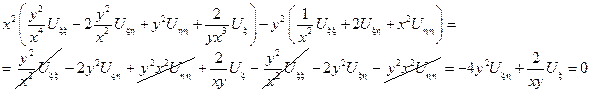
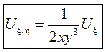 канонический вид гиперболического типа.
канонический вид гиперболического типа.
2-ой случай: Приведение к каноническому виду уравнения параболического типа.
В этом случае дискриминант = 0.
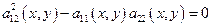 для любой
для любой 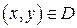 из R2.
из R2.
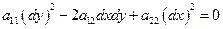
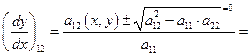
Единственное решение характеристического уравнения:
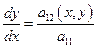 , т.е. существует единственная функция
, т.е. существует единственная функция 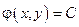 такая, что
такая, что
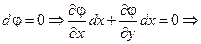
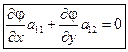
Поскольку 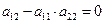 , то
, то
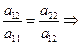
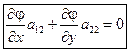
Выбор замены переменных в случае уравнения параболического типа:
В параболическом случае в качестве 1-ой функции замены переменной выбираем функцию 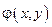 , а в качестве 2-ой функции – производную функцию
, а в качестве 2-ой функции – производную функцию 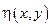 , такую что якобиан замены переменных отличен от нуля, то есть
, такую что якобиан замены переменных отличен от нуля, то есть
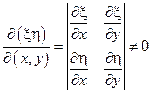 ,
,
тогда
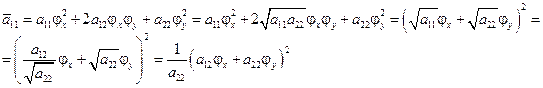
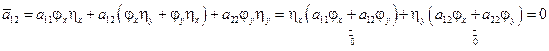
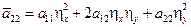 – аналогично покажем =
– аналогично покажем =
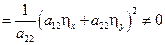
Следовательно канонический вид уравнения параболического вида следующий:
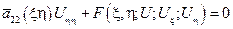
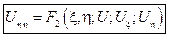 канонический вид уравнения параболического типа.
канонический вид уравнения параболического типа.
1) 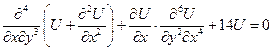
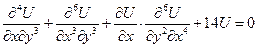
уравнение 6-ого порядка
6 – порядок
3) Найти области гиперболической, эллиптической
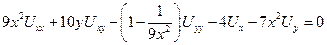
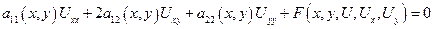
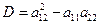
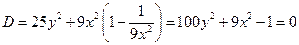
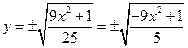
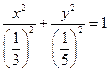
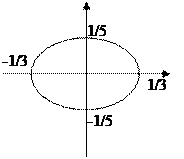
Параболичность
D < -1 – внутри эллипса эллиптичность
Снаружи эллипса – гиперболичность
3) 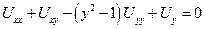
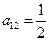
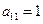
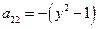
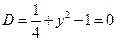
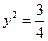
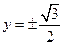
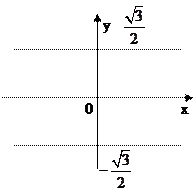
Внутри – эллиптичность
Снаружи – гиперболичность
3) 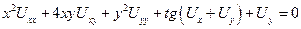
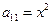
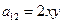
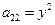
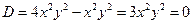

4) 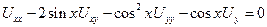
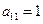
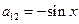
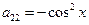
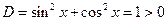
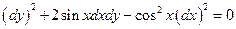
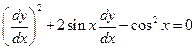
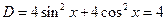
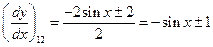
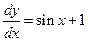
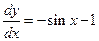
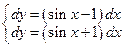
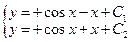
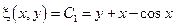
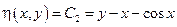
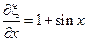
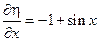
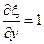
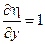
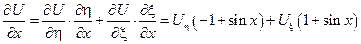
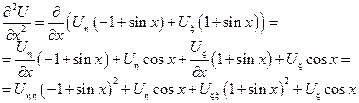
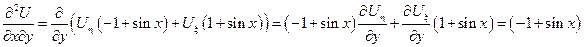
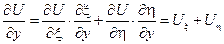
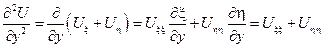
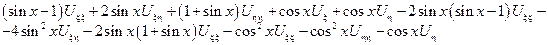
Нужно раскрыть скобки, привести подобные и получить канонический вид.
21.02.08
Пример параболическая:
Привести к каноническому виду уравнение 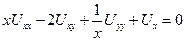 .
.
Определим тип уравнения:
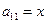
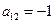
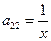
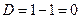 – параболический тип уравнения.
– параболический тип уравнения.
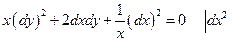
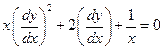
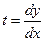
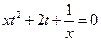
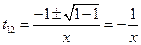
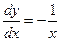
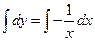
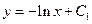
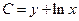
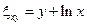
Составим якобиан с заменой переменных
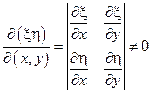
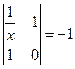
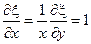
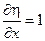
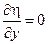
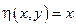 , следовательно выбрана замена переменных
, следовательно выбрана замена переменных
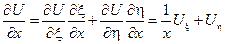
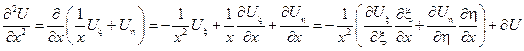
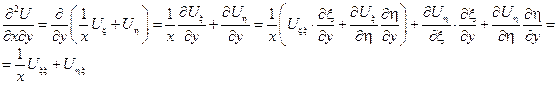
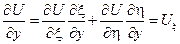
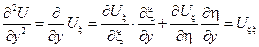
Подставим найденные производные в исходное уравнение:
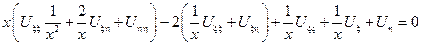
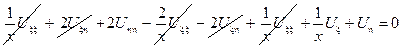
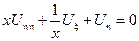
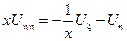
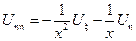 – канонический вид уравнения параболического типа.
– канонический вид уравнения параболического типа.
Приведение к каноническому виду уравнений эллиптического типа
Случай 3
D < 0
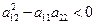 составим уравнение характеристик.
составим уравнение характеристик.
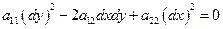
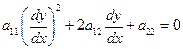
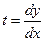
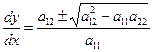
последнее уравнение имеет комплексное аналитическое решение
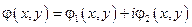 , где
, где
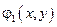 – действительная часть решения,
– действительная часть решения,
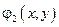 – мнимая часть решения.
– мнимая часть решения.
Замена:
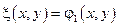
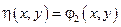
Можно показать, что
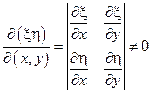
Функция 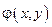 является решением уравнения
является решением уравнения
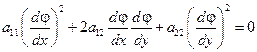
См. случай 2
Откуда получаем, что
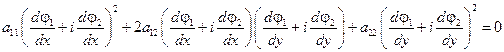
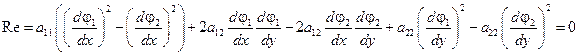
Откуда вытекает (см. случай 1) (выражение для коэффициентов 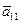 ,
, 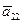
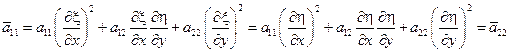
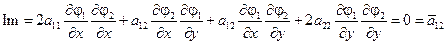
Следовательно, в новых переменных уравнение приобретает вид:
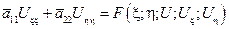
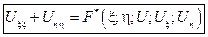 канонический вид уравнения эллиптического типа.
канонический вид уравнения эллиптического типа.
Пример:
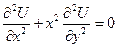 .
.
Решение:
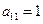
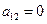
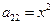
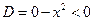 – уравнение эллиптического типа, если x ≠ 0.
– уравнение эллиптического типа, если x ≠ 0.
Уравнение характеристик
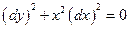
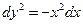
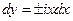
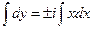
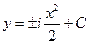 →
→ 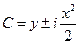
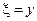
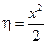
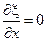
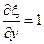
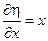
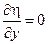
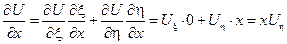
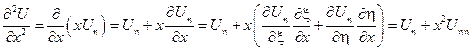
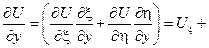
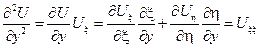
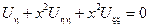
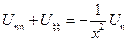
1. Гиперболические уравнения
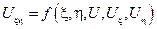
2. Параболические уравнения
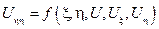
3. Эллиптические уравнения
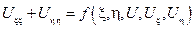
Дата добавления: 2015-02-28; просмотров: 6423;
