Постановка волновых задач для волнового уравнения
1 задача: «Задача Коми»
Замечание: Волновое уравнение имеет бесконечно много решений. Решение становится единственным как только на искомое решение будут наложены некоторые условия, обуславлив. поведение изучаемого физ. объекта (струна, стержень…) В начальный момент времени, начальное полож., скорость струны (стержня).
Поведение концов струны в зависимости от времени (стержня), сила действующая на концах струны (стержне).
Все эти условия приводят к тому, что решение становится единственным.
Постановка задачи Коми и краевых задач
| Задача Коми | 1-ая краевая задача | 2-ая краевая задача |
1. 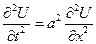 t >0
t >0 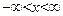 Однородная задача рассматр. струна бесконечная
U(x,0)=f(x) – условие задающее положение струны в начальный момент времени
Ut(x,0)=g(x) – скорость струны в начальный момент времени (нет воздействия внешних сил)
Однородная задача рассматр. струна бесконечная
U(x,0)=f(x) – условие задающее положение струны в начальный момент времени
Ut(x,0)=g(x) – скорость струны в начальный момент времени (нет воздействия внешних сил)
| 1. Однородная 1-ая краевая задача
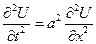 t >0
t >0 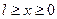 U(x,0)=f(x)
Начальное отклонение
Ut(x,0)=g(x) – начальная скорость
U(0,t)=μ(t) – закон. движение левого конца струны с течением времени
U(l,t)=μ2(t) – закон движения правого конца струны
U(x,0)=f(x)
Начальное отклонение
Ut(x,0)=g(x) – начальная скорость
U(0,t)=μ(t) – закон. движение левого конца струны с течением времени
U(l,t)=μ2(t) – закон движения правого конца струны
| 1. Однородная 2-ая краевая задача
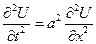 t >0
t >0 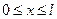 U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)=
U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)= 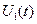 - сила действия на левый конец струны течением времени вдоль оси ОХ
Ux(l,t)= - сила действия на левый конец струны течением времени вдоль оси ОХ
Ux(l,t)= 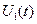 - сила действия на правый конец струны вдоль ОХ - сила действия на правый конец струны вдоль ОХ
|
2. Неоднородная задача
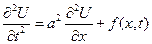 t >0
t >0 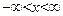 U(x,0)=f(x) – нач. положение
Ut(x,0)=g(x) есть воздействие внешних сил
U(x,0)=f(x) – нач. положение
Ut(x,0)=g(x) есть воздействие внешних сил
| 2. 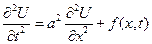 U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)=U(l,t)=0 - лев. и прав. концы закрепления
U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)=U(l,t)=0 - лев. и прав. концы закрепления
| 2. Неоднородная задача
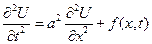 U(x,0)=f(x)
Ut(x,0)=g(x)
Ux(0,t)=Ux(l,t)=0 - вдоль оси концы не смещ. (однород. краев. услов. 2-ого типа
U(x,0)=f(x)
Ut(x,0)=g(x)
Ux(0,t)=Ux(l,t)=0 - вдоль оси концы не смещ. (однород. краев. услов. 2-ого типа
|
1,2 – первые краевые условия
Если U(0,t)=U(l,t)=0 – заданы 1-ые краевые условия однородные
3, 4 – краев. условия 2-ого типа для волнового уравнения
3-я задача краевого типа
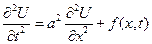 t >0
t >0 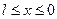
U(x,0)=f(x)
Ut(x,0)=g(x)
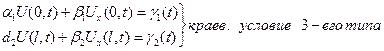
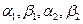 - заданные числа
- заданные числа
Краевые условии 1-ого типа описывают траектории движения левого и правого концов
Краевые условия 2-ого типа описывают силы, воздействующие на левый и правый концы, при этом в 1-ом случае не учитывается воздействие сил на концы, во 2-ом – не учитываются траектории их движения; краевые условия 3-его типа учитывают и то и другое.
Задача Коши для волнового уравнения
1. Приведение одновременного волнового уравнения к канонической форме и его решение

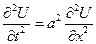
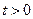
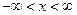
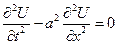
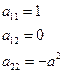
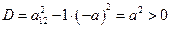 – уравнение гиперболического типа
– уравнение гиперболического типа
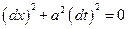
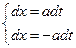
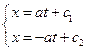
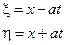
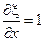
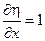
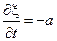
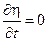
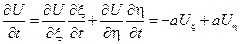
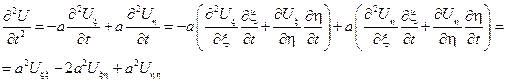
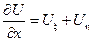
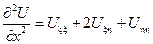
………
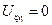
Общим решением полученного уравнения будет являться решение
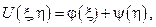 где
где
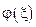 и
и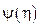 -любые дифференцируемые произвольные функции.
-любые дифференцируемые произвольные функции.
Заменяя ξ и η на их определение, получаем общее решение волнового уравнения в виде
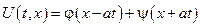
С физической точки зрения это решение интересно тем, что представляет собой сумму 2-х бегущих волн, движущихся в противоположных направлениях со скоростью а.
2. Решение Даламбера одномерного однородного волнового уравнения
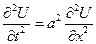
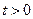
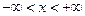
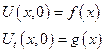
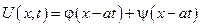 - определим функции φ и ψ однозначным образом, исходя из начальных условий
- определим функции φ и ψ однозначным образом, исходя из начальных условий
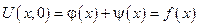
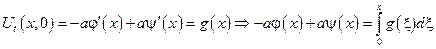
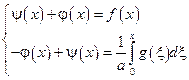
сложим: 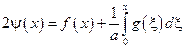
вычитаем: 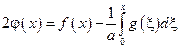
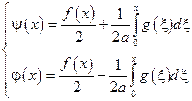
Подставим найденное выражение в общее решение исходного однородного уравнения:
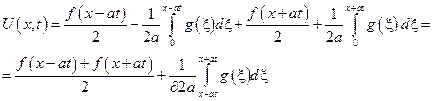
- решение однородной задачи Коши для бесконечной струны (формула Даламбера).
3. Неоднородная задача
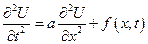
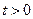
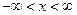
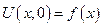
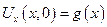
Будем искать решение в виде суммы 2-х функций.
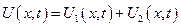
1) 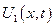 - решение однородной задачи
- решение однородной задачи
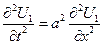
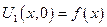
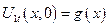
2) 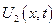 - решение неоднородной задачи с однородными краевыми условиями
- решение неоднородной задачи с однородными краевыми условиями
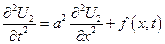
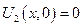
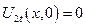
Решение 1-ой задачи – формула Даламбера
2-я задача решение:
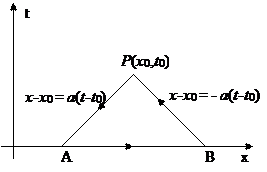
|
Уравнения прямой: 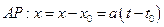
Уравнения прямой: 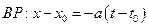
От обеих частей уравнения
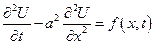 - возьмем интеграл по области R
- возьмем интеграл по области R
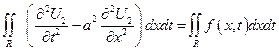
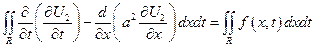
по формуле Грина (Стокса)
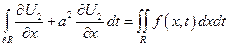
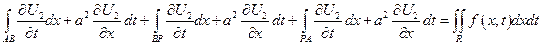
На 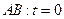
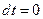
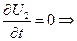
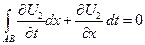
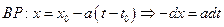
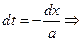
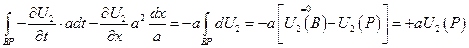
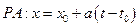
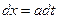
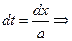
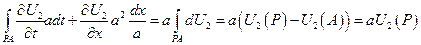
Подставляем в исходное уравнение
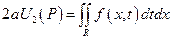 разделим на 2а:
разделим на 2а:
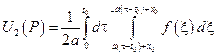
Следовательно, искомое решение неоднородного уравнения имеет вид: Римана – Вольтера
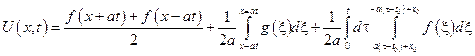
№8 Пример: Решить задачу Коши
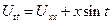
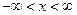
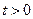
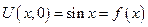
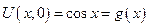
a = 1
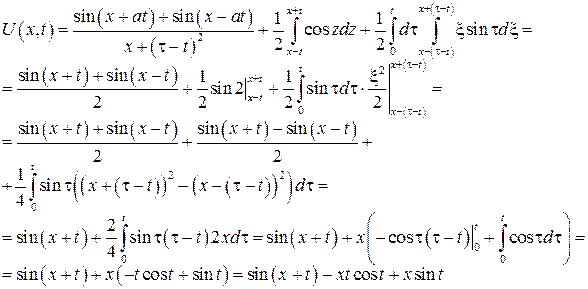
Дата добавления: 2015-02-28; просмотров: 4072;
