Уравнение малых продольных колебаний упругого стержня

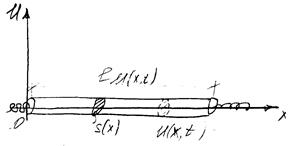
Рассмотрим стержень, расположенный вдоль оси ОХ, введем обозначения:

S(x) – площадь сечения стержня плоскостью, перпендикулярной ОХ,

k(x) и ρ(x) – модуль Юнга и плотность сечения с абсциссой х,

U(x,t) – величина отклонения сечения (вдоль стержня) с абсциссой х в момент времени t.

При этом предполагается, что величина отклонений всех точек сечения одинакова. Рассмотрим малые продольные колебания.

Малые – такие продольные колебания, при которых возникающее натяжение подчиняется закону Гука.

Подсчитаем фигурирующие формулировки закона Гука, относительно удлинения участка от х до х+Δх в момент времени t:

,

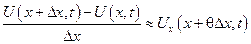тогда

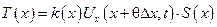
Пусть f(x,t) – плотность равнодействующих внешних сил, действующих на сечение с абсциссой х вдоль оси ОХ. По закону сохранения энергии изменение количества движения участка стержня [x₁, x₂] за время 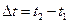равно импульсу действующих сил, которые в рассматриваемом случае складываются из сил натяжения Т(x) и внешних сил

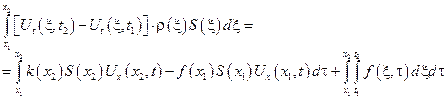
- это уравнение малых продольных колебаний стержня в интегральной форме в рамках описанной выше модели.

Если сравнить с уравнением колеб. малой поперечной струны в интегральной форме они почти ничем не отличаются переход от интегральной к диференц. происходит аналогично.

Предположение, что U(x,t)- дважды непрерывно дифференцир., T(x), S(x), k(x) –непрерывн. производн. 1-го порядка, по теореме Лагранжа о конечных приращен и по интегральн. теореме о среднем получаем, как и выше

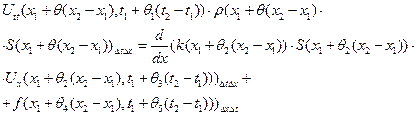
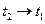
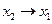
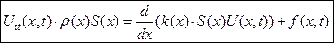
малых продольных колебаний стержня

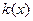- модуль Юнга

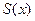- площадь перпендикулярного поперечного сечения

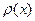- плотность сечения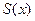

Будем считать

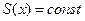
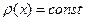
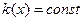
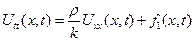
Положим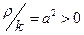

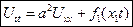
Уравнение малых поперечных колебаний мембраны (двумерное волновое уравнение)

Мембраной называется натянутая плоская пленка не сопротивл. изгибу и сдвигу.

Но оказывает сопротивление растяжению. Будем рассматривать малые поперечные колебания мембраны, в которых смещен. перпендикуляр плоскости ОХУ и квадратами величин Ux и Uy можно пренебречь в сравнении с 1

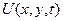величина смещения точки (х,у) в момент времени t

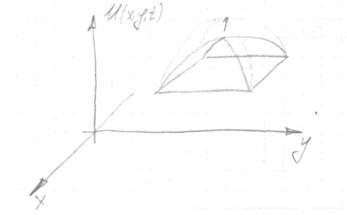
dS – элемент дуги некоторого контура, лежащего на поверхности мембраны.

Пусть М точка этого элемента на которой действует сила натяжения TdS. Отсутствие сопротивления мембраны изгибу и сдвигу математически выражается в том, что вектор натяж. Т лежит в плоскости касательной мембраны в т. М и 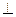элементу dS, а величина натяжения Т не зависит от направления элемента dS, содержащего т. М.

Из этого вытекает

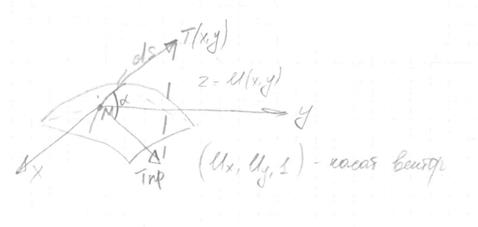
1. Проекция вектора натяжения на плоскость ОХУ = Т_пр

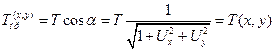
2. Сила натяжения Т не зависит от времени t

Найдем площадь возмущенной мембраны

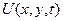- функция задающая возмущен. мембрану в момент времени t, тогда

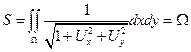
- проекция кусочка возмущенной мембраны на пл-ть ОХУ

Площадь возмущения куска мембраны = S невозмущен., т.е. площадь фиксированного участка мембраны не смещается со временем (участок не растягивается).

В силу закона Гука сила натяжен. Т не зависит от времени t

3. Сила натяжения Т не зависит не от х не от у

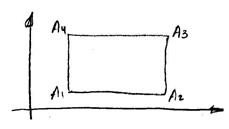
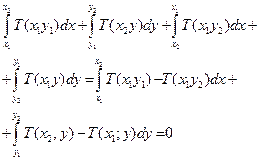
Причем последнее равенство выполнено для любых точек x₁; x₂ и y₁; y₂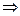

Т(x,y₁) = Т(x,y₂) и Т(x₁,y) = Т(x₂,y)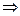

Т(x,y) не зависит не от х и не от у

Получим уравнение малых поперечных колебаний мембраны:

Общее количество движения:

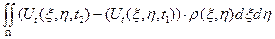
f(x,y,t) – плотность равнодействующей внешних сил, действующих на мембрану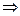

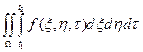- работа соверш. внешними силами

Работа, которую совершает сила натяжения, за время от t₁ до t₂ будет равна

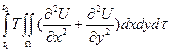
По закону сохранения энергии получаем уравнение

-

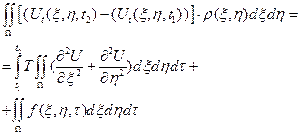Это и есть уравнение малых поперечных мембран в интегрированной форме

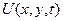- дважды непрерывно дифференц.

По теореме о среднем и по теореме Лагранжа, получаем как и выше диф. уравнение малых поперечных колебаний мембраны

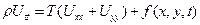- двумерное волновое уравнение

Вообще говоря гипербол. типа