Уравнение полных поперечных колебаний струны
Струна – упругая нить, не сопротивляющаяся изгибу, но оказывающая сопротивление растяжению, т.е. напряжение, возникающее в струне, всегда направлено по касательной к ее ???новенному профилю. Будем считать, что струна расположена вдоль оси ОХ. Движение струны происходит только в одной плоскости, в этой плоскости каждая точка струны движется в направлении, перпендикулярном оси ОХ. Функция смещения струны U(x,t) – величина отклонения точки струны с координатой x в момент времени t, угловые коэффициенты касательной к линии прогиба достаточно малы, т.е. струна совершает малые колебания.
|
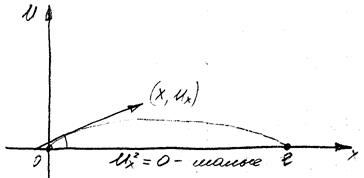
U(x,t) – функция положения струны
Построим дифференциальное уравнение, которому будет удовлетворять функция U(x,t).
В момент времени t длина струны: 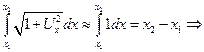 длина струны не меняется со временем (струна не растяжима) => по закону Гука величина силы натяжения струны не меняется со временем, т.е.
длина струны не меняется со временем (струна не растяжима) => по закону Гука величина силы натяжения струны не меняется со временем, т.е.
Т = Т(х) – сила натяжения струны зависит только от х.
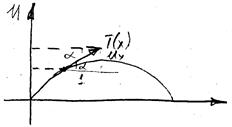
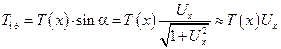
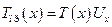
На струну могут действовать внешние силы, обозначим f(x,t) – плотность равнодействующих внешних сил, действующих на струну в направлении оси OU.
Общее количество движения.
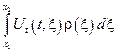 – количество движений струны или работа, которую совершает струна в данный момент времени (на отрезке [x1, x2]) → 1)
– количество движений струны или работа, которую совершает струна в данный момент времени (на отрезке [x1, x2]) → 1)
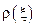 – точечная плотность струны
– точечная плотность струны
1) Под воздействием силы натяжения и внешних сил
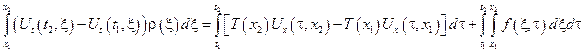 – уравнение малых поперечных колебаний струны в интегральной форме, т.к. функция U(x,t) дважды непрерывно дифференцируема.
– уравнение малых поперечных колебаний струны в интегральной форме, т.к. функция U(x,t) дважды непрерывно дифференцируема.
Т(х) – непрерывно дифференцируема.
По теории Лагранжа о конечных приращениях:
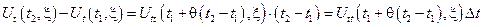
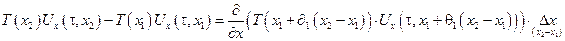
где 0 < (θ и θ1) < 1.
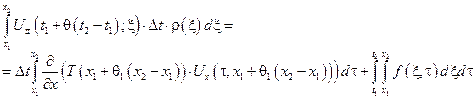
Воспользуемся теоремой о среднем значении для интеграла Римана
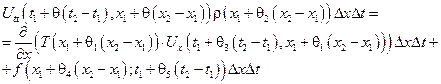
Разделим обе части равенства на 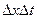 и устремим t2 → t1, x2 → x1.
и устремим t2 → t1, x2 → x1.
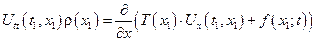
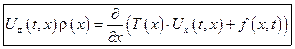
уравнение малых колебаний поперечной струны
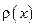 – точечная плотность струны
– точечная плотность струны
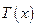 – сила натяжения струны в т. х
– сила натяжения струны в т. х
В случае, когда 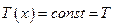 ,
, 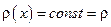
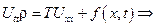
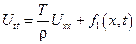 , обозначим
, обозначим 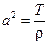
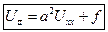 уравнение малых поперечных колебаний струны.
уравнение малых поперечных колебаний струны.
Очевидно, что уравнение является квазилинейным
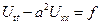
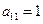
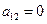
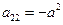
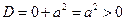 – уравнение гиперболического типа и называется – одномерное волновое уравнение.
– уравнение гиперболического типа и называется – одномерное волновое уравнение.
Дата добавления: 2015-02-28; просмотров: 1061;

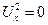 – малые
– малые