ПРИМЕР 9

Для другого примера оценки линии тренда и сезонного регулирования мы заимствовали сведения из госпиталя, которые использовали 66-месячные данные о взрослых стационарных больных, и получили следующее уравнение:

Y = 8091+21,5Х,

где Y— пациенто-дни; X— время, мес.

На базе этой модели госпиталь прогнозирует пациенто-дни для следующего месяца (период 67):

Пациенто-дни = 8091 + 21.5 (67) = 9530 (только используя тренд).

Так как эта модель определяет линию возрастающего тренда в спросе на обслуживание пациентов, она игнорирует сезонность, которая на сегодня известна администрации. Таблица, приведенная ниже, содержит текущие сезонные индек­сы, базирующиеся на тех же 66 месяцах. Такие сезонные данные, как эти, являются типичными для госпиталей. Заметим, что в январе, марте, июле и августе прояв­ляются особенно высокие в среднем количества пациенто-дней, а февраль, сен­тябрь, ноябрь и декабрь показывают снижение количества пациенто-дней.

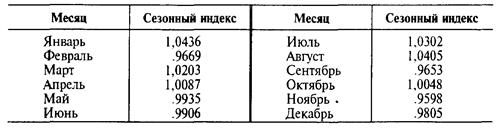
Корректируя временные серии экстраполяцией с учетом сезонности, госпи­таль умножает месячный прогноз на соответствующий сезонный индекс. Так, дляпериода 67, которым был январь,

Пациенто-дни = (9530)( 1.0436) = 9946 (тренд с учетом сезонности).

Используя этот метод, были спрогнозированы пациенто-дни с января по июнь (периоды с 67 по 72) как 9946, 9236, 9768, 9678, 9554 и 9547. В этом примере лучше прогнозируются пациенто-дни, так же как более точно прогнозируются бюджетные расходы.

6. МЕТОДЫ РЕГРЕССИОННОГО

И КОРРЕЛЯЦИОННОГО АНАЛИЗОВ

Модели причинного прогнозирования обычно содержат ряд переменных, которые имеют отношение к предсказываемой пере­менной. Как только эти переменные будут найдены, строится статистическая модель, которая используется для прогноза инте­ресующей нас переменной. Этот подход является более мощным, чем методы временных серий, которые используют прошлые зна­чения для прогнозируемой переменной.

Многие факторы могли бы рассматриваться в причинном анализе. Например, продажи товара могут быть связаны с расхо­дами фирмы на рекламу, с назначаемой ценой, с делами конку­рентов и стратегиями продвижения товаров или даже с экономи­ческими условиями и безработицей. В этом случае продажи буду! называться зависимой переменной, а другие переменные буду" называться независимыми переменными. Работа менеджеров за­ключается в установлении наилучшей статистической зависимос­ти между продажами и независимыми переменными. Наиболее общей количественной моделью причинного прогнозирована является модель линейного регрессионного анализа.

Использование регрессионного анализа для прогнозирования. Мы можем использовать такие математические модели, ко­торые применяли как метод наименьших квадратов в трендовом проектировании, преобразовав их к моделям линейной регрессии Зависимая переменная, которую мы хотим спрогнозировать, будет обозначаться у. Но теперь независимая переменная х — это не время.

у = а + bх,

где у —значение зависимой переменной, здесь — объем продаж;

а — отрезок, отсекаемый на оси у,

b — наклон линии регрессии;

х— независимая переменная.