ПРИМЕР 10
Строительная компания реконструирует старые дома. По истечении времени компания нашла, что ее объем работ по реконструкции связан с уровнем местной заработной платы. Таблица ниже содержит данные о годовых доходах и суммах денежных доходов в 1987—1992 голах.
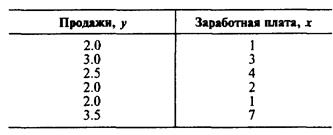
Служба менеджмента компании хочет представить математическую взаимосвязь, которая будет помогать ей предсказывать продажи. Первое, что необходимо определить, имеет ли место линейная связь между заработной платой и продажами; для этого наносятся известные данные на диаграмму рассеивания.
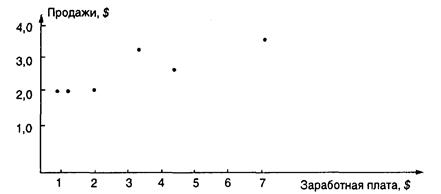
На диаграмме показано шесть точек данных, которые отражают положительную зависимость между независимой переменной, заработной платой и зависимой переменной, продажами. Когда зарплата возрастает, продажи компании имеют тенденцию к повышению.
Мы можем найти математическое уравнение регрессии, используя метод наименьших квадратов.


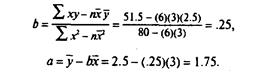
Уравнение регрессии, следовательно, будет:
у =1.75 +.25х,
или:
Продажи = 1,75 + .25 Зарплата.
Если местная коммерческая служба определит, что зарплата в регионе будет $ 600 000 000 в следующем году, мы можем прогнозировать продажи строительной компании по уравнению регрессии:
Продажи (в млн $) = 1.75 + .25 (6)
или:
Продажи = $325 000.
Заключительная часть примера 10 иллюстрирует главную слабость методов прогнозирования на базе регрессии. Даже когда мы рассчитали уравнение, необходимо проводить прогноз независимой переменной х (в этом случае заработной платы), прежде чем определять зависимую переменную у для следующего периода времени. Хотя это — проблема не для всех прогнозов, следует представлять себе сложности в определении будущих значений таких общих независимых переменных, как уровень безработицы, валовой национальный продукт, индексы цен и т. д.
Прогноз продаж $325 000 в примере 10 называется точкой оценки для у. Точка оценки является реальным значением, или ожидаемой величиной, возможных объемов продаж дистрибьюторов. Рис. 4.6 иллюстрирует этот подход.
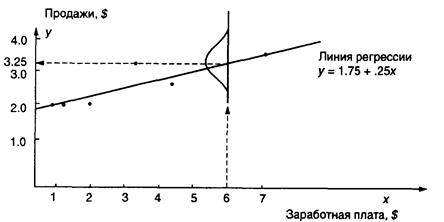
Рис. 4.6. Стандартная ошибка отклонения
Измеряя точность регрессионных оценок, нам необходимо рассчитать стандартную ошибку прогноза Sy,x. Ее называют стандартным отклонением уравнения регрессии. Уравнение (4.11) мы находим в большинстве книг по статистике для расчета стандартного отклонения арифметических значений:
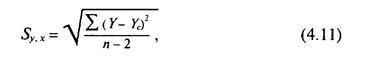
где Y — значение Y для каждой точки данных;
Yc — расчетное значение зависимой переменной из уравнения регрессии;
п — число точек данных.
Уравнение (4.12) может показаться более общим, но это только версия уравнения (4.11). Та и другая формулы требуют общих данных и могут быть использованы на прогнозируемых интервалах вокруг оцениваемой точки.
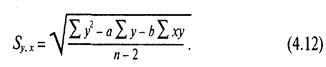

Коэффициенты корреляции для линии регрессии. Уравнение регрессии — это один из путей установления природы взаимосвязи между двумя переменными. Уравнение показывает, как одна переменная отражается на значении и изменениях другой переменной.
Другой путь установления отношений между двумя переменными заключается в расчёте коэффициентов корреляции. Этот измеритель показывает степень, или силу, линейной взаимосвязи. Обычно обозначаемый как r, коэффициент корреляции может быть некоторым числом между +1 и -1. Рис. 4.7 иллюстрирует различные возможные значения r.
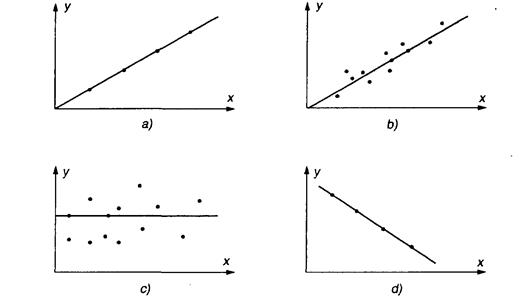
рис. 4.7. Четыре значения коэффициента корреляции:
а) положительная корреляция г = +1; Ь} положительная корреляция 0 <<• < 1:
с) нет корреляции г = 0; с1) отрицательная корреляция г = -1
Рассчитывая r, мы используем много тех данных, которые необходимы для расчета а и b в уравнении регрессии. Более протяженное уравнение для r следующее:
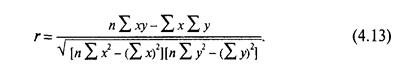
Дата добавления: 2015-01-13; просмотров: 863;
