ПРИМЕР 12

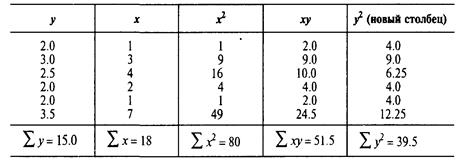
В примере 10 мы показали взаимосвязь между заказами строительной компа­нии и уровнем заработной платы. Рассчитывая коэффициенты корреляции для указанных данных, мы можем только суммировать один расчетный столбец (для y²) и затем обращаться к уравнению для г

Множественный регрессионный анализ. Множественная регрессия — это практически расширение модели, которую мы толь­ко что рассматривали. Она позволяет строить модель с рядом независимых переменных. Например, если строительная компа­ния хочет включать среднюю годовую процентную ставку в ее модель прогноза продаж, соответствующее уравнение будет:

у = а + b₁x₁+b₂x₂ (4.14)

где у — зависимая переменная, продажи;

а — отрезок, отсекаемый на оси у;

x₁ и x₂ — значения двух независимых переменных: зарплаты и процентной ставки соответственно.

Математически множественная регрессия требует комплекса средств (обычно с применением компьютера), а формулу для определения а, b₂ и b₂ мы находим в учебниках по статистике.

ПРИМЕР 13

Новая линия регрессии, рассчитанная по компьютерной программе, для стро­ительной компании имеет вид равенства:

Y=1,80 +.30X₁ +5.0X₂.

Мы также находим, что новый коэффициент корреляции .96, означающий включение переменной Хг, процентной ставки даже более усиливает линейную зависимость.

Мы можем теперь прогнозировать продажи компании, если знаем значения заработной платы и процентной ставки в следующем году. Если зарплата будет $600 млн и рыночная ставка .12 (12%), продажи будут прогнозироваться как

Продажи (5 сотни тысяч) = 1.80 + .30(6) - 5.0(.12) = 1.8 + 1.8 - .6 = 3.00, или

Продажи = $300 000.